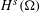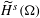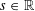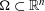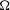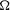This paper provides an overview of interpolation of Banach and Hilbert spaces, with a focus on establishing when equivalence of norms is in fact equality of norms in the key results of the theory. (In brief, our conclusion for the Hilbert space case is that, with the right normalizations, all the key results hold with equality of norms.) In the final section we apply the Hilbert space results to the Sobolev spaces 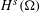$H^{s}({\rm\Omega})$ and 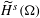$\widetilde{H}^{s}({\rm\Omega})$, for 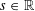$s\in \mathbb{R}$ and an open 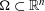${\rm\Omega}\subset \mathbb{R}^{n}$. We exhibit examples in one and two dimensions of sets 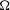${\rm\Omega}$ for which these scales of Sobolev spaces are not interpolation scales. In the cases where they are interpolation scales (in particular, if 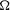${\rm\Omega}$ is Lipschitz) we exhibit examples that show that, in general, the interpolation norm does not coincide with the intrinsic Sobolev norm and, in fact, the ratio of these two norms can be arbitrarily large.

We give a simple direct proof of the interpolation inequality $ \|\nabla f\|^2_{L^{2p}} \le C \|f\|_{\rm BMO} \|f\|_{W^{2,p}}$, where $ 1<p<\infty$. For $p=2$ this inequality was obtained by Meyer and Rivière via a different method, and it was applied to prove a regularity theorem for a class of Yang–Mills fields. We also extend the result to higher derivatives, sharpening all those cases of classical Gagliardo–Nirenberg inequalities where the norm of the function is taken in $L^\infty$ and other norms are in $L^q$ for appropriate $q>1$.

The asymptotic behaviour of entropy numbers of Trudinger–Strichartz embeddings of radial Besov spaces on ${\mathbb R}^n$ into exponential Orlicz spaces is calculated. Estimates of the entropy numbers as well as estimates of entropy numbers of Sobolev embeddings of radial Besov spaces are applied to spectral theory of certain pseudo-differential operators.