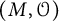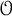1 Introduction
Sheets in a reductive algebraic group G are the irreducible components of the locally closed subsets of G consisting of conjugacy classes of the same dimension. They occur also as irreducible components of the strata in the partition of G, defined in [Reference Lusztig, Nevins and Trapa10] in terms of Springer representations with trivial local system (see [Reference Carnovale2, Reference Carnovale3]). One of the most fascinating features of strata is that they are parametrized by a family of irreducible representations of the Weyl group which depends on the root system of G and not on the characteristic of the base field. It is therefore of interest to figure out the behavior of the irreducible components of strata when the characteristic of the base field varies.
A description of sheets in good characteristic, and a parametrization of sheets in terms of G-conjugacy classes of triples
$(M, Z(M)^{\circ } s, {\mathcal O})$
where M is the identity component of the centralizer of a semisimple element in G,
$Z(M)^{\circ } s$
is a suitable coset in the component group
$Z(M)/Z(M)^{\circ }$
, and
${\mathcal O}$
is a rigid unipotent conjugacy class in M was given in [Reference Carnovale and Esposito4] in good characteristic, and extended to the case of bad characteristic in [Reference Simion14]. A refinement of this parametrization in terms of pairs
$(M,{\mathcal O})$
where M and
${\mathcal O}$
are as above was given in [Reference Carnovale3] under the assumption that G is simple of adjoint type and the characteristic of the base field is good for G. The present paper answers a question by G. Lusztig on the extension to arbitrary characteristic of this parametrization of sheets.
Observe that, even if the formulation of the statement is the same, the collection of possible centralizers of a semisimple element in G varies with the characteristic of the base field, as well as the collection of unipotent conjugacy classes. Centralizers of semisimple elements are fewer in bad characteristic than in good characteristic (see [Reference Carter5–Reference Deriziotis8]), whereas the number of unipotent conjugacy classes may increase when passing from good to bad characteristic.
We therefore elaborate upon results in [Reference Carter5, Reference Carter6, Reference Deriziotis8] in the spirit of [Reference McNinch and Sommers13] in order to provide a combinatorial description of the root systems of connected centralizers of semisimple elements, which will allow us to retrieve most ingredients that were necessary for the proof of [Reference Carnovale3, Theorem 4.1]. As an example, we show that the number of sheets in type
$G_2$
is the same in good characteristic and in characteristic
$3$
, but it is smaller in characteristic
$2$
, showing a difference in the behavior of sheets as opposed to strata.
2 Notation
Let G be a connected reductive algebraic group defined over an algebraically closed field k of characteristic exponent p. Let
$\Phi $
be the root system of G, and let
$\Delta =\{\alpha _1,\,\ldots ,\,\alpha _n\}$
be a fixed base of
$\Phi $
. If
$\Phi $
is irreducible, the numbering of simple roots will be as in [Reference Bourbaki1] and we will denote by
$\alpha _0$
the opposite of the highest root in
$\Phi $
and by
$d_i$
the coefficient of
$\alpha _i$
in the expression of
$-\alpha _0$
. We set
$d_0:=1$
and
$\widetilde {\Delta }=\Delta \cup \{\alpha _0\}$
. For a subset
$S\subset \widetilde {\Delta }$
, we define
$d_S:=\mathrm {gcd}(d_i~|~\alpha _i\not \in S)$
. In particular,
$d_S=1$
if
$S\subset \Delta $
.
The group acts on itself by conjugation and we denote
$g\cdot h=ghg^{-1}$
for
$g,\,h\in G$
and
$G\cdot g$
the G-conjugacy class of
$g\in G$
. For a closed subgroup
$H\leq G$
, the identity component will be denoted by
$H^{\circ }$
, and for
$g\in G$
the centralizer will be denoted by
$G_g$
. We will call
$G_g^{\circ }$
the connected centralizer of g. The Jordan decomposition of an element
$g\in G$
will be usually denoted by
$g=su$
.
For
$m\in {\mathbb N}$
, we set
$G_{(m)}:=\{g\in G~|~\dim (G\cdot g)=m\}$
. These sets are locally closed and their irreducible components are called the sheets of the G-action. For
$Z\subset G$
, we also define
$m_Z:=\max \{m\in {\mathbb N}~|~G_{(m)}\cap Z\neq \emptyset \}$
and
$Z^{reg}:=Z\cap G_{(m_Z)}$
, and
$C_G(Z)$
will indicate the centralizer of Z in G.
If we fix a maximal torus T of G and
$\Phi $
is the root system of G with respect to T, then for
$\alpha \in \Phi $
, we indicate by
$X_{\alpha }$
the corresponding root subgroup. For a closed subset
$\Psi \subset \Phi $
(see [Reference Bourbaki1, Chapter VI, n. 1.7, Définition 4]), and for
$s\in T$
, we set
$G_{\Psi }:=\langle T,\,X_{\alpha }~|~\alpha \in \Psi \rangle $
.
2.1 Construction of sheets and a first parametrization
It was observed in [Reference Lusztig9, Section 3] that G has a partition into finitely many, locally closed, smooth, irreducible, G-stable sets, which we call Jordan classes, each contained in some
$G_{(m)}$
. As a set, the class containing
$g=su$
is
$$ \begin{align*} J(su)=G\cdot((Z(G^{\circ}_s)^{\circ} s)^{reg}u). \end{align*} $$
In other words, a G-conjugacy class lies in
$J(su)$
if and only if it contains an element with Jordan decomposition
$s'u$
with
$G^{\circ }_{s}=G^{\circ }_{s'}$
and
$s'\in Z(G^{\circ }_s)^{\circ } s$
. The closure of a Jordan class is a union of Jordan classes (see [Reference Lusztig9, Section 3]); hence, the same holds for the regular locus of the closure of a Jordan class. This gives a partial order on the set of Jordan classes given by
$J_1\leq J_2$
if and only if
$J_1\subset \overline {J_2}^{reg}$
. The sheets in G are the locally closed sets of the form
$\overline {J}^{reg}$
where J is maximal with respect to
$\leq $
. Hence, the set of sheets in G is in bijection with the set
$\mathcal {J}$
consisting of maximal Jordan classes (see [Reference Carnovale and Esposito4, Proposition 5.1], [Reference Simion14, Section 3]).
If
$J=J(su)$
as above, then [Reference Carnovale3, Lemma 2.1] and [Reference Carnovale and Esposito4, Proposition 4.8] give
$$ \begin{align*} \overline{J(su)}^{reg}&=\bigcup_{z\in Z(G_s^{\circ})^{\circ} s}G\cdot(z\mathrm{Ind}_{G_s^{\circ}}^{G_z^{\circ}}(G_s^{\circ}\cdot u)), \end{align*} $$
where
$\mathrm {Ind}_{G_s^{\circ }}^{G_z^{\circ }}(G_s^{\circ }\cdot u)$
is Lusztig–Spaltenstein’s induced unipotent conjugacy class (see [Reference Lusztig and Spaltenstein11]). The maximal Jordan classes are precisely those for which the class of u is rigid in
$G_s^{\circ }$
, i. e., it is not induced from any unipotent class in a proper Levi subgroup of a parabolic subgroup of
$G_s^{\circ }$
(see [Reference Carnovale and Esposito4, Proposition 5.3], [Reference Simion14, Lemma 2.4]).
Sheets are then parametrized as follows.
Theorem 2.1 ([Reference Carnovale and Esposito4, Theorem 5.6], [Reference Simion14, Theorem 3.1])
The assignment
$J=J(su)\mapsto (G_s^{\circ }, Z(G_s^{\circ })^{\circ } s, G_s^{\circ }\cdot u)$
induces a bijection between
${\mathcal J}$
and the set of G-orbits of triples
$(M,Z(M)^{\circ } r,{\mathcal O})$
where M is the connected centralizer of a semisimple element of G;
$Z(M)^{\circ } r$
is a coset in
$Z(M)/Z(M)^{\circ }$
satisfying
$C_G(Z(M)^{\circ } r)^{\circ }=M$
and
${\mathcal O}$
is a rigid unipotent conjugacy class in M.
We aim at a simpler parametrization for G simple and of adjoint type.
2.2 Connected centralizers of semisimple elements
In this subsection, G is quasisimple. Identity components of centralizers of semisimple elements have been studied in [Reference Carter5–Reference Deriziotis8, Reference McNinch and Sommers13]. In the spirit of the latter, we give a combinatorial characterization of the root subsystem of such subgroups when the base field is an arbitrary algebraically closed field.
Proposition 2.2 Let G be quasisimple, let T be a maximal torus in G, and let
$\Psi $
be a closed subset of
$\Phi $
. Then
$G_{\Psi }$
is the connected centralizer of an element in T if and only if
$\Psi $
is conjugate to a root subsystem
$\Psi '$
admitting a base
$\Delta _{\Psi '}\subset \widetilde {\Delta }$
and such that
$\mathrm { gcd}(p,\,d_i~|~i\in \widetilde {\Delta }\setminus \Delta _{\Psi '})=1$
by an element in the normalizer
$N(T)$
of T.
Proof If
$\Psi $
is
$N(T)$
-conjugate to a root subsystem
$\Psi '$
admitting a base
$\Delta _{\Psi '}\subset \widetilde {\Delta }$
and such that
$\mathrm {gcd}(p,\,d_i~|~i\in \widetilde {\Delta }\setminus \Delta _{\psi '})=1$
, then there exists an
$\alpha _{\overline {i}} \in \widetilde {\Delta }\setminus \Delta _{\Psi '}$
such that
$p\not |d_{\overline {i}}$
. Replacing
$a_1$
with
$d_{\overline {i}}$
in the proof of [Reference McNinch and Sommers13, Proposition 32], we obtain an element
$s\in Z(G_{\Psi })$
such that
$G_s^{\circ }=G_{\Psi' }$
.
Assume now that
$G_{\Psi }=G_s^{\circ }$
for some
$s\in T$
. By [Reference McNinch and Sommers13, Proposition 30], the subgroup
$G_{\Psi }$
is G-conjugate to some
$G_{\Psi '}$
where
$\Psi '$
admits a base
$\Delta _{\Psi '}\subset \widetilde {\Delta }$
. Conjugacy of maximal tori in
$G_{\Psi '}$
ensures that conjugation of the two subgroups, and of the corresponding root systems can be obtained using an element in
$N(T)$
. We show that
$\mathrm {gcd}(p, d_{\Delta _{\Psi '}})=1$
. If the characteristic exponent
$p=1$
, then there is nothing to prove. Assume for a contradiction that
$p>1$
and divides
$d_i$
for every
$\alpha _i\in \widetilde {\Delta }\setminus \Delta _{\Psi '}$
. Since
$d_0=1$
, in this situation
$\alpha _0\in \Delta _{\Psi '}$
and
$G_{\Psi '}$
is never the Levi subgroup of a parabolic subgroup of G.
Let
$\{\omega _j^{\vee },\,j=1,\,\ldots ,\,n\}$
be the basis for the cocharacters of T dual to
$\Delta $
, and let
$t\in T$
be such that
$G_{\Psi '}=G_t^{\circ }$
. Since
$\alpha _i(t)=1$
, for every
$\alpha _i\in \Delta _{\Psi '}$
, we have
$t=\prod _{j=1,\ldots ,\,n\atop \alpha _j\not \in \Delta _{\Psi' }}\omega _j^{\vee }(\zeta _j)$
, and
$\alpha _0(t)=1$
gives
$$ \begin{align} \prod_{j\geq 1,\, \alpha_j\not\in\Delta_{\Psi'}}\zeta_j^{d_j}=1, \textrm{ so also } \prod_{j\geq 1,\, \alpha_j\not\in\Delta_{\Psi'}}\zeta_j^{d_j/p^l}=1\textrm{ if }p^l|d_{\Delta_{\Psi'}}. \end{align} $$
By [Reference Bourbaki1, Section 1 of Chapter VI, n. 1.7, Paragraphe 1.7, Proposition 24], the system
$\Psi '$
is not
${\mathbb Q}$
-closed, i.e., there exists an
$\alpha \in \left ({\mathbb Q}\Delta _{\Psi '}\cap \Phi \right )\setminus \Psi '$
. In other words, there exist
$a,\,b,\, a_i,\,b_i\in {\mathbb Z}$
, for
$i=1,\,\ldots ,\,n$
such that
$\alpha _i\not \in \Delta _{\Psi '}$
, with
$b, b_i\neq 0$
and
$z_j\in {\mathbb Z}$
for
$j=1,\,\ldots ,\,n$
such that
$$ \begin{align*} \alpha=\frac{a}{b}\alpha_0+\sum_{\alpha_i\in\Delta_{\Psi'}\cap\Delta}\frac{a_i}{b_i}\alpha_i=\sum_{j=1}^nz_j\alpha_j\in\Phi\setminus\Psi'. \end{align*} $$
Hence,
$b|d_i$
for all
$\alpha _i\not \in \Delta _{\Psi '}$
, that is,
$b|d_{\Delta _{\Psi '}}$
. Observe that
$d_{\Delta _{\Psi '}}$
is either
$p^l$
for some
$l\geq 1$
or else
$d_{\Delta _{\Psi '}}=6$
,
$\Phi =E_8$
,
$p=2$
or
$3$
, and
$\Delta _{\Psi '}=\widetilde {\Delta }\setminus \{\alpha _4\}$
. In the first case, (2.1) gives
$\alpha (t)=1$
, a contradiction. In the second case,
$t=\omega ^{\vee }_4(\zeta _4)$
and (2.1) becomes
$\zeta _4^{6/p}=1$
. Let
$\beta \in \Phi \setminus \Psi '$
be such that its coefficient of
$\alpha _4$
in its expression as a sum of simple roots is
$6/p$
. Then again
$\beta (t)=1$
, a contradiction.
Remark 2.3 The coprimality condition in Proposition 2.2 says that the centralizers we lose when passing from good characteristic to bad characteristic p are precisely those subgroups that in good characteristic are connected centralizers of elements of order divisible by p. When k is the algebraic closure of a finite field the statement could also be extracted from [Reference Deriziotis7, Section 2].
Proposition 2.4 Let G be simple of adjoint type, let T be a maximal torus in G, and let
$\Psi \subset \Phi $
be a closed subsystem such that
$G_{\Psi }=G_s^{\circ }$
for some
$s\in T$
. Assume in addition that
$\Psi $
admits a base
$\Delta _{\Psi }\subset \widetilde {\Delta }$
. Then:
-
(a) The torsion subgroup of
${\mathbb Z}\Phi /{\mathbb Z}\Psi $
is
${\mathbb Z}/d_{\Delta _{\Psi }}{\mathbb Z}$
. -
(b)
$Z(G_{\Psi })/Z(G_{\Psi })^{\circ }$
is cyclic of order
$d_{\Delta _{\Psi }}$
. -
(c) For
$t\in Z(G_{\Psi })$
, we have
$C_G(Z(G_{\Psi })^{\circ } t)=G_{\Psi }$
if and only if
$Z(G_{\Psi })^{\circ } t$
is a generator of
$Z(G_{\Psi })/Z(G_{\Psi })^{\circ }$
.
Proof
-
(a) This is observed in [Reference Sommers15, Section 2].
-
(b) The order of the torsion subgroup of
${\mathbb Z}\Phi /{\mathbb Z}\Psi $
is coprime with p by Proposition 2.2. Hence, we are in a position to use the argument in [Reference McNinch and Sommers13, Lemma 33] and [Reference Sommers15, Section 2.1], that we sketch for completeness. By construction and [Reference Malle and Testerman12, Proposition 3.8] from which we borrow notation,
$Z(G_{\Psi })=({\mathbb Z}\Psi )^{\perp }$
,
$Z(G_{\Psi })^{\perp }={\mathbb Z}\Psi $
, and the character group
$X(Z(G_{\Psi }))$
is
${\mathbb Z}\Phi /{\mathbb Z}\Psi $
. Then consists of those torsion elements in
$$ \begin{align*}X(Z(G_{\Psi})/Z(G_{\Psi})^{\circ})\simeq\{\chi\in X(Z(G_{\Psi}))~|~\chi(z)=1,\,\forall z\in Z(G_{\Psi})^{\circ}\}\end{align*} $$
${\mathbb Z}\Phi /{\mathbb Z}\Psi $
whose order is coprime with p, that is,
${\mathbb Z}/d_{\Delta _{\Psi }}{\mathbb Z}$
.
-
(c) In good characteristic, this is, [Reference McNinch and Sommers13, Lemma 34(1)], whose proof relies on the fact that every character of
$Z(G_{\Psi })/Z(G_{\Psi })^{\circ }$
can be represented by an element in
$\Phi $
. The proof of this statement depends on considerations on root systems which are characteristic-free and on a natural isomorphism between
$X(Z(G_{\Psi })/Z(G_{\Psi })^{\circ })$
and
${\mathbb Z}({\mathbb Q}\Psi \cap \Phi )/{\mathbb Z}\Psi $
, which remains valid because
$X(Z(G_{\Psi })/Z(G_{\Psi })^{\circ })$
is the torsion subgroup of
${\mathbb Z}\Phi /{\mathbb Z}\Psi $
also in our situation.
2.3 The parametrization
In this subsection, G is simple of adjoint type. We are now in a position to prove the refinement of the parametrization of sheets of G. The general case can be readily deduced by standard arguments.
Theorem 2.5 Let G be simple and of adjoint type. The sheets in G are in bijection with the G-conjugacy classes of pairs
$(M,{\mathcal O})$
where M is the connected centralizer of a semisimple element in G and
${\mathcal O}$
is a rigid unipotent conjugacy class in M.
Proof In good characteristic, this is [Reference Carnovale2, Theorem 4.1], so we assume that p is bad for G. Sheets are parametrized by triples
$(M, Z(M)^{\circ } s,{\mathcal O})$
as in Theorem 2.1. The assignment
$(M, Z(M)^{\circ } s,{\mathcal O})\mapsto (M,\,{\mathcal O})$
induces a well-defined and surjective map between the set of G-conjugacy classes of triples and the set of G-conjugacy classes of pairs as above. We show injectivity of this map. If G is classical, then M is a Levi subgroup of a parabolic subgroup of G, for any pair
$(M,{\mathcal O})$
; hence,
$Z(M)=Z(M)^{\circ }$
and there is nothing to prove, so we assume that G is of exceptional type.
Let
$(M,Z(M)^{\circ } s,{\mathcal O})$
and
$(M,Z(M)^{\circ } r,{\mathcal O})$
be two triples inducing the same image. Without loss of generality
$s\in T$
,
$M=G_{\Psi }$
where
$\Psi $
has base
$\Delta _{\Psi }\subset \widetilde {\Delta }$
, and
$Z(M)^{\circ } s,\,Z(M)^{\circ } r\subset T$
. If
$d_{\Delta _{\Psi }}\leq 2$
, then necessarily
$Z(M)^{\circ } r= Z(M)^{\circ } s$
, so we assume that
$d_{\Delta _{\Psi }}\geq 3$
.
By [Reference Sommers15, Proposition 7], there is a w in the stabilizer
$N_W(\Delta _{\Psi })$
of
$\Delta _{\Psi }$
in W whose action on
${\mathbb Z}\Phi /{\mathbb Z}\Psi $
generates the automorphism group of the torsion subgroup of
${\mathbb Z}\Phi /{\mathbb Z}\Psi $
, which is isomorphic to
$Z(M)/Z(M)^{\circ }$
by Proposition 2.4(a). We claim that any representative of w in
$N(T)$
preserves
${\mathcal O}$
. Since rigid unipotent classes in type A are trivial, it is enough to consider only the case in which
$\Delta _{\Psi }$
contains a (necessarily unique) component of type different from A, and
${\mathcal O}$
is nontrivial in the corresponding subgroup. Such a component is always preserved by the action of w. The list of
$\Delta _{\Psi }$
with
$d_{\Delta _{\Psi }}\geq 3$
in the proof of [Reference Sommers15, Proposition 7] shows that we only need to consider two cases for G of type
$E_8$
, namely
$\Delta _{\Psi }=A_3+ D_5$
which may occur only when
$p=3,5$
, and
$\Delta _{\Psi }=A_2+ E_6$
. Unipotent conjugacy classes in type D for
$p=3$
and
$5$
are characteristic unless their Jordan form corresponds to a very even partition, i.e., a partition with only even terms, each occurring an even number of times. Such partitions never occur in
$D_n$
for n odd.
Rigid unipotent conjugacy classes in
$E_6$
in arbitrary characteristic can be deduced from [Reference Spaltenstein16, Chapitre II. Appendice] and they are characteristic for dimensional reasons.
Fixing a maximal torus T in G, by standard arguments, we retrieve a parametrization of sheets by orbits of the Weyl group. We set
${\mathcal T}$
to be the set of pairs
$(M,{\mathcal O})$
where M is the connected centralizer of an element in T and
${\mathcal O}$
is a rigid unipotent class in M, so
$N(T)$
and
$W=N(T)/T$
naturally act on
$\mathcal {T}$
.
Corollary 2.6 Let G be simple and of adjoint type. The sheets in G are parametrized by elements in
${\mathcal T}/W$
.
Remark 2.7 If the characteristic of the base field is good, replacing “rigid” by “distinguished” in the parametrization in Theorem 2.5 one obtains the parametrization of conjugacy classes in the component group of the centraliser of unipotent conjugacy classes in G in [Reference McNinch and Sommers13, Reference Sommers15]. In bad characteristic, the most naive generalization of this parametrization fails to hold, as there are too few connected centralizers of semisimple elements, and it would be interesting to detect a suitable analog.
2.4 On the number of sheets in G
It was observed in [Reference Simion14, Remark 3.3] that for G of type
$B_2$
, the number of sheets is independent of the characteristic and it was suggested this to hold in general for G connected and simply connected. This fails in general because there exist sheets that are obtained from one another by multiplication by a central element, and such central element might no longer exist in bad characteristic: for example, in
$G=SL_2(k)$
, the sheets are:
$\{{\mathrm {id}}\}$
,
$\{-{\mathrm {id}}\}$
, and
$G^{reg}$
for
$p\neq 2$
, and
$\{{\mathrm {id}}\}$
and
$G^{reg}$
for
$p=2$
. The following remark shows that the number of sheets depends on p also for G simple of adjoint type.
Remark 2.8 Let
$\Phi =G_2$
. We use the parametrization in Theorem 2.5. The semisimple parts of the connected centralizers for p good are of type:
$G_2$
,
$A_2$
,
$A_1+\widetilde {A}_1$
,
$A_1$
,
$\widetilde {A}_1$
or conjugate to T. In type A, all rigid unipotent classes are trivial, and there are three rigid unipotent classes in G (see [Reference Spaltenstein16, Chapitre II. Appendice]). Hence, there are eight sheets for p good.
According to Proposition A.1, the semisimple parts of the connected centralizers for
$p=2$
are of type:
$G_2$
,
$A_2$
,
$A_1$
,
$\widetilde {A}_1$
or conjugate to T, and there are three rigid unipotent classes in G (see [Reference Spaltenstein16, Chapitre II. Appendice]). Hence, there are seven sheets for
$p=2$
.
According to Proposition A.1, the semisimple parts of the connected centralizers for
$p=3$
are of type:
$G_2$
,
$A_1+\widetilde {A}_1$
,
$A_1$
,
$\widetilde {A}_1$
or conjugate to T, and there is an extra unipotent conjugacy class in
$G_2$
which is rigid, as it can be deduced from the list of induced classes in [Reference Spaltenstein16, Chapitre II. Appendice]. Hence, the number of sheets for
$p=3$
equals the number of sheets for p good.
A Appendix
For the reader’s convenience, we list the possible connected centralizers in bad characteristic. When k is the closure of a finite field this list appeared in [Reference Deriziotis7, pp. 25–27]. For writing the Table A.1, we made use of the analysis of W-conjugacy classes of subsets of
$\widetilde {\Delta }$
in [Reference Sommers15, Section 2.2]. In most cases, these classes are determined by their isomorphism type and the root lengths. For
$\Phi =E_7$
and
$E_8$
, we remove ambiguities adopting, as in loc. cit., Dynkin’s convention. Namely, for
$n= 7,8$
, we decorate with one prime the root subsystems which can be embedded in the subsystem of type
$A_n$
within
$E_n$
, whereas we decorate with two primes the root subsystems with the same label which cannot be embedded in
$A_n \subset E_n$
.
Table A.1 Root subsystems to be discarded.
Proposition A.1 Let G be quasisimple with p bad for G. Let T be a maximal torus in G and
$\Psi \subset \Phi $
be a closed subsystem with base
$\Delta _{\Psi }\subset \widetilde {\Delta }$
.
If
$\Phi $
is of classical type, then
$G_{\Psi }$
is the connected centralizer of an element in T if and only if it is the Levi subgroup of a parabolic subgroup of G (see [Reference Carter6]).
If
$\Phi $
is of exceptional type, then
$G_{\Psi }$
is the connected centralizer of an element in T unless
$G,\,p$
and
$\Psi $
occur in Table A.1.
In other words, the subsystems to be discarded are those containing the subsystem whose base consists of all elements in
$\widetilde {\Delta }$
whose coefficient in the expression of
$-\alpha _0$
is not divisible by p.
Acknowledgment
We wish to thank Prof. G. Lusztig for asking the question leading to this short note, Prof. J. Michel for pointing us reference [Reference Deriziotis7], and the referee for his/her remark on centralizers and the appendix table.
