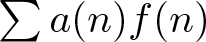1. Introduction
In number theory and many other branches of mathematics, distributions of finite sums of arithmetic functions constitute an active area of interest. An important tool for calculating the finite sum of a given arithmetic function is a summation formula of the form
 \begin{align}
\sideset{}{'}\sum_{a\leq n\leq b}f(n)=\int_{a}^{b}f(x)\,dx+2\sum_{n=1}^{\infty}\int_{a}^bf(x)\cos(2\pi n x)\,dx.
\end{align}
\begin{align}
\sideset{}{'}\sum_{a\leq n\leq b}f(n)=\int_{a}^{b}f(x)\,dx+2\sum_{n=1}^{\infty}\int_{a}^bf(x)\cos(2\pi n x)\,dx.
\end{align} Here the function f can be taken as a function of bounded variation that is supported in a finite compact interval and the dash on the sum indicates that the last term of the sum is multiplied by ![]() $\frac{1}{2}$ if n = b. The Gauss circle problem and the Dirichlet divisor problem are two well-known problems in this direction. Dirichlet showed that if d(n) denotes the number of positive divisors of an integer n, then
$\frac{1}{2}$ if n = b. The Gauss circle problem and the Dirichlet divisor problem are two well-known problems in this direction. Dirichlet showed that if d(n) denotes the number of positive divisors of an integer n, then
 \begin{align*}
\Delta_d(x):=\sum_{n\leq x}d(n)-x\log x-(2\gamma -1)x=O(x^{1/2}).
\end{align*}
\begin{align*}
\Delta_d(x):=\sum_{n\leq x}d(n)-x\log x-(2\gamma -1)x=O(x^{1/2}).
\end{align*} On the other hand, if ![]() $r_2(n)$ is the number of ways to represent a positive integer n as a sum of squares of two integers then Gauss showed that
$r_2(n)$ is the number of ways to represent a positive integer n as a sum of squares of two integers then Gauss showed that
 \begin{align*}
\Delta_r(x)=\bigg\lvert\sum_{n\leq x}r_2(n)-\pi x\bigg\rvert=O(x^{1/2}).
\end{align*}
\begin{align*}
\Delta_r(x)=\bigg\lvert\sum_{n\leq x}r_2(n)-\pi x\bigg\rvert=O(x^{1/2}).
\end{align*} Much later, in 1904, Voronoï [Reference Voronoï40, Reference Voronoï41] generalized the summation formula (1.1) to improve the bounds for ![]() $\Delta_d(x)$ and
$\Delta_d(x)$ and ![]() $\Delta_r(x)$ to
$\Delta_r(x)$ to ![]() $O(x^{1/3})$. In particular, he obtained in [Reference Voronoï40]
$O(x^{1/3})$. In particular, he obtained in [Reference Voronoï40]
 \begin{align}
\sideset{}{'}\sum_{a\leq n \leq b}d(n)f(n)=\int_a^bf(x)(\log x+2\gamma)\,dx+\sum_{n=1}^{\infty}d(n)\int_a^bf(x)L_0(4\pi\sqrt{nx})\,dx
\end{align}
\begin{align}
\sideset{}{'}\sum_{a\leq n \leq b}d(n)f(n)=\int_a^bf(x)(\log x+2\gamma)\,dx+\sum_{n=1}^{\infty}d(n)\int_a^bf(x)L_0(4\pi\sqrt{nx})\,dx
\end{align}and
 \begin{align}
\sideset{}{'}\sum_{a\leq n \leq b}r_2(n)f(n)=\pi\sum_{n=1}^{\infty}r_2(n)\int_a^bf(x)J_0(2\pi\sqrt{nx})\,dx,
\end{align}
\begin{align}
\sideset{}{'}\sum_{a\leq n \leq b}r_2(n)f(n)=\pi\sum_{n=1}^{\infty}r_2(n)\int_a^bf(x)J_0(2\pi\sqrt{nx})\,dx,
\end{align} where f is a piecewise monotonic and continuous function, ![]() $L_0(x):=4K_0(x)-2\pi Y_0(x)$, K 0 is the modified Bessel function of the second kind, and
$L_0(x):=4K_0(x)-2\pi Y_0(x)$, K 0 is the modified Bessel function of the second kind, and ![]() $J_0, Y_0$ are Bessel functions of the first and second kind respectively.
$J_0, Y_0$ are Bessel functions of the first and second kind respectively.
Voronoï summation is the best known method for improving the bounds for ![]() $\Delta_d(x)$ and
$\Delta_d(x)$ and ![]() $\Delta_r(x$) and was crucial in understanding the lower bounds of these two error terms. By using (1.2) and (1.3), Hardy and Landau observed in [Reference Hardy and Landau28] that
$\Delta_r(x$) and was crucial in understanding the lower bounds of these two error terms. By using (1.2) and (1.3), Hardy and Landau observed in [Reference Hardy and Landau28] that ![]() $\Delta_d(x)$ and
$\Delta_d(x)$ and ![]() $\Delta_r(x)$ cannot be
$\Delta_r(x)$ cannot be ![]() $O(x^{1/4})$. Consequently, they conjectured that both
$O(x^{1/4})$. Consequently, they conjectured that both ![]() $\Delta_d(x)$ and
$\Delta_d(x)$ and ![]() $\Delta_r(x)$ are
$\Delta_r(x)$ are ![]() $O_\epsilon(x^{1/4+\epsilon})$ for any ϵ > 0.
$O_\epsilon(x^{1/4+\epsilon})$ for any ϵ > 0.
Returning to the work in [Reference Voronoï40, Reference Voronoï41], Voronoï found a common pattern in the proofs of (1.2) and (1.3). This led him to propose analogous summation formulas of the type (1.2) and (1.3) for  $\sum_{a\leq n\leq b}a(n)f(n)$, where a(n) is any ‘arithmetic function’ and f(n) is a ‘nice’ test function. Without evidence, it is generally accepted that a(n) is chosen to be the coefficient of some known L-function in order to produce analogues of the Voronoï summation formula. The choices for a(n) now also include automorphic forms as seen in [Reference Goldfeld and Li22], [Reference Miller and Schmid34], etc. The selection of the test function f(n) is an important component of the Voronoï summation formula. Ideally, one would like to choose discontinuous characteristic functions as candidates for f(n), since one is primarily interested in the partial sum
$\sum_{a\leq n\leq b}a(n)f(n)$, where a(n) is any ‘arithmetic function’ and f(n) is a ‘nice’ test function. Without evidence, it is generally accepted that a(n) is chosen to be the coefficient of some known L-function in order to produce analogues of the Voronoï summation formula. The choices for a(n) now also include automorphic forms as seen in [Reference Goldfeld and Li22], [Reference Miller and Schmid34], etc. The selection of the test function f(n) is an important component of the Voronoï summation formula. Ideally, one would like to choose discontinuous characteristic functions as candidates for f(n), since one is primarily interested in the partial sum  $\sum_{a\leq n\leq b}a(n)$. However, one notes that smooth functions serve as good approximations to these test functions and due to the rapid decay of smooth functions, the integral transforms on the right-hand side of the summation formula (analogous to those on the right-hand side of (1.2) or (1.3)) can be analysed well. On the other hand, due to the approximation error, a small amount of information is lost when a characteristic function is replaced by a smooth function.
$\sum_{a\leq n\leq b}a(n)$. However, one notes that smooth functions serve as good approximations to these test functions and due to the rapid decay of smooth functions, the integral transforms on the right-hand side of the summation formula (analogous to those on the right-hand side of (1.2) or (1.3)) can be analysed well. On the other hand, due to the approximation error, a small amount of information is lost when a characteristic function is replaced by a smooth function.
The main objective of this article is to revisit the coefficients a(n) in the Voronoï summation formula. We consider a broad class ![]() $\mathcal{C}$ of Dirichlet series satisfying functional equations of Hecke-type and derive analogues of the Voronoï summation formula for coefficients of these series. While results in this direction have been obtained in a lot of generality, the key aspect of this article is that we demonstrate the converse. More precisely, we show that if an ‘arithmetic function’ a(n) satisfies such a Voronoï-type summation formula, then it must appear as a coefficient of some Dirichlet series within this general class. In particular, we prove an equivalence between the functional equation of Hecke-type for the Dirichlet series corresponding to a(n) and the analogue of the Voronoï summation formula for a(n). While there are multiple results in various settings for the forward implication (that is, showing that the functional equation implies a summation formula), the converse is not known in much generality. We elaborate more upon this in §1. The converse is usually proved via an identity known as a modular relation (see for instance (1.20)). A unique feature of our result is that in order to prove this converse for our general L-function, we give an auxiliary modular relation which is different from the one occurring naturally for our Dirichlet series and has not appeared in the literature previously. Moreover, we show that this new modular relation is equivalent to the functional equation.
$\mathcal{C}$ of Dirichlet series satisfying functional equations of Hecke-type and derive analogues of the Voronoï summation formula for coefficients of these series. While results in this direction have been obtained in a lot of generality, the key aspect of this article is that we demonstrate the converse. More precisely, we show that if an ‘arithmetic function’ a(n) satisfies such a Voronoï-type summation formula, then it must appear as a coefficient of some Dirichlet series within this general class. In particular, we prove an equivalence between the functional equation of Hecke-type for the Dirichlet series corresponding to a(n) and the analogue of the Voronoï summation formula for a(n). While there are multiple results in various settings for the forward implication (that is, showing that the functional equation implies a summation formula), the converse is not known in much generality. We elaborate more upon this in §1. The converse is usually proved via an identity known as a modular relation (see for instance (1.20)). A unique feature of our result is that in order to prove this converse for our general L-function, we give an auxiliary modular relation which is different from the one occurring naturally for our Dirichlet series and has not appeared in the literature previously. Moreover, we show that this new modular relation is equivalent to the functional equation.
Modular identities have a rich history, going back to the ubiquitous Poisson summation formula, which serves as the basis for them. The Poisson summation formula is expressed as
 \begin{align*}
\sum_{n\in\mathbb{Z}}f(n)=\sum_{n\in\mathbb{Z}}\hat{f}(n)
\end{align*}
\begin{align*}
\sum_{n\in\mathbb{Z}}f(n)=\sum_{n\in\mathbb{Z}}\hat{f}(n)
\end{align*} for all Schwartz functions f. Here  $\hat{f}(t):=\int_{\mathbb{R}}f(x)e^{-2\pi i t x}\,dx$ is the Fourier transform of f. If one considers the function
$\hat{f}(t):=\int_{\mathbb{R}}f(x)e^{-2\pi i t x}\,dx$ is the Fourier transform of f. If one considers the function  $f(x)=e^{-\pi x^2 t}$, t > 0, then we have the well-known modular identity, also called the θ-identity:
$f(x)=e^{-\pi x^2 t}$, t > 0, then we have the well-known modular identity, also called the θ-identity:
 \begin{align*}
\theta(t):=\sum_{n\in\mathbb{Z}}e^{-\pi n^2 t}=\frac{1}{\sqrt{t}}\sum_{n\in\mathbb{Z}}e^{-\frac{\pi n^2}{t}}, \quad (t \gt 0).
\end{align*}
\begin{align*}
\theta(t):=\sum_{n\in\mathbb{Z}}e^{-\pi n^2 t}=\frac{1}{\sqrt{t}}\sum_{n\in\mathbb{Z}}e^{-\frac{\pi n^2}{t}}, \quad (t \gt 0).
\end{align*} It was based on this identity that Riemann [Reference Riemann36] in his landmark memoir built the theory of the zeta function and derived the functional equation of ![]() $\zeta(s)$. Results obtaining the θ-identity from the functional equation were given by Cahen [Reference Cahen14], Hamburger [Reference Hamburger23–Reference Hamburger26], and Hurwitz (unpublished note, cf. [Reference Oswald35]).
$\zeta(s)$. Results obtaining the θ-identity from the functional equation were given by Cahen [Reference Cahen14], Hamburger [Reference Hamburger23–Reference Hamburger26], and Hurwitz (unpublished note, cf. [Reference Oswald35]).
In order to state our results, we recall the Riesz-mean sum:  $\sideset{}{'}\sum_{n\leq x}a(n)(x-n)^{\rho}$, with
$\sideset{}{'}\sum_{n\leq x}a(n)(x-n)^{\rho}$, with ![]() $\rho\ge 0$, where the dash on the sum indicates that the last term of the sum has to be multiplied by
$\rho\ge 0$, where the dash on the sum indicates that the last term of the sum has to be multiplied by ![]() $\frac{1}{2}$ if ρ = 0 and x = n. After the work of Ramanujan on
$\frac{1}{2}$ if ρ = 0 and x = n. After the work of Ramanujan on ![]() $\tau(n)$ (defined by
$\tau(n)$ (defined by ![]() $\sum_{n=1}^{\infty}\tau(n)z^n=z\prod_{n=1}^{\infty}(1-z^n)^{24}$ for
$\sum_{n=1}^{\infty}\tau(n)z^n=z\prod_{n=1}^{\infty}(1-z^n)^{24}$ for ![]() $|z| \lt 1$), Wilton [Reference Wilton42] considered the Riesz sum
$|z| \lt 1$), Wilton [Reference Wilton42] considered the Riesz sum  $\sideset{}{'}\sum_{n\leq x}\tau(n)(x-n)^{\rho}$ and obtained the summation formula
$\sideset{}{'}\sum_{n\leq x}\tau(n)(x-n)^{\rho}$ and obtained the summation formula
 \begin{align}
A_{\rho}(x):=\frac{1}{\Gamma(\rho +1)}\sideset{}{'}\sum_{n\leq x}\tau(n)(x-n)^{\rho}=\left(\frac{1}{2\pi}\right)^{\rho}\sum_{n=1}^{\infty}\left(\frac{x}{n}\right)^{6+\rho/2}\tau(n)J_{12+\rho}(4\pi\sqrt{nx})
\end{align}
\begin{align}
A_{\rho}(x):=\frac{1}{\Gamma(\rho +1)}\sideset{}{'}\sum_{n\leq x}\tau(n)(x-n)^{\rho}=\left(\frac{1}{2\pi}\right)^{\rho}\sum_{n=1}^{\infty}\left(\frac{x}{n}\right)^{6+\rho/2}\tau(n)J_{12+\rho}(4\pi\sqrt{nx})
\end{align}for ρ > 0. Hardy [Reference Hardy27] improved this result and proved that ρ can be taken to be 0. This is the most desirable case. Recall that for any suitable smooth test function f, partial summation gives
 \begin{align}
\sideset{}{'}\sum_{n\leq x}\tau(n)f(n)=A_0(x)f(x)-\int_1^xA_0(t)f'(t)\,dt.
\end{align}
\begin{align}
\sideset{}{'}\sum_{n\leq x}\tau(n)f(n)=A_0(x)f(x)-\int_1^xA_0(t)f'(t)\,dt.
\end{align} Substituting the infinite series representation of ![]() $A_0(t)$ from (1.4) into this and performing some elementary computations yields analogues of the Voronoï summation formula. Although the right-hand side of (1.4) converges absolutely and uniformly in any compact interval for large values of ρ, it can be seen to be convergent by some other means for small values of ρ. If we denote
$A_0(t)$ from (1.4) into this and performing some elementary computations yields analogues of the Voronoï summation formula. Although the right-hand side of (1.4) converges absolutely and uniformly in any compact interval for large values of ρ, it can be seen to be convergent by some other means for small values of ρ. If we denote  $S(x)=\sideset{}{'}\sum_{n\leq x} a(n)$ and
$S(x)=\sideset{}{'}\sum_{n\leq x} a(n)$ and  $S_1(x)=\sideset{}{'}\sum_{n\leq x} a(n)(x-n)$ for a general arithmetic function a(n), then by partial summation, one has
$S_1(x)=\sideset{}{'}\sum_{n\leq x} a(n)(x-n)$ for a general arithmetic function a(n), then by partial summation, one has  $S_1(x)=\int_1^x S(t)\, dt$. Since the infinite series representation of
$S_1(x)=\int_1^x S(t)\, dt$. Since the infinite series representation of ![]() $S_1(x)$ (analogous to the right-hand side of (1.4)) converges rapidly and analysing the series is relatively simple, bounding S(x) in terms of
$S_1(x)$ (analogous to the right-hand side of (1.4)) converges rapidly and analysing the series is relatively simple, bounding S(x) in terms of ![]() $S_1(x)$ is fruitful. This is a key reason for studying Reisz sums. Moreover, if S(x) is monotonic then one can bound S(x) by the difference
$S_1(x)$ is fruitful. This is a key reason for studying Reisz sums. Moreover, if S(x) is monotonic then one can bound S(x) by the difference ![]() $S_1(x)-S_1(x(1\pm \delta))$ for some suitable choice of δ.
$S_1(x)-S_1(x(1\pm \delta))$ for some suitable choice of δ.
We now state our main results below. We will consider a class ![]() $\mathcal{C}$ of Dirichlet series with a more general functional equation with multiple Gamma factors. This class is defined as follows.
$\mathcal{C}$ of Dirichlet series with a more general functional equation with multiple Gamma factors. This class is defined as follows.
Definition 1.1. We say that ![]() $\phi(s), \psi(s) \in \mathcal C$ if
$\phi(s), \psi(s) \in \mathcal C$ if
(1)
 $ \phi(s)$ and
$ \phi(s)$ and  $ \psi(s)$ are as defined in (1.18) with finite abscissae of absolute convergence σa and σb respectively.
$ \psi(s)$ are as defined in (1.18) with finite abscissae of absolute convergence σa and σb respectively.(2)
 $\phi(s)$ and
$\phi(s)$ and  $\psi(s)$ satisfy a functional equation of the type
(1.6)
$\psi(s)$ satisfy a functional equation of the type
(1.6) \begin{equation}
Q^sF(s)=\omega Q^{{\delta}-s} \overline{G({\delta}-\bar{s})},
\end{equation}
\begin{equation}
Q^sF(s)=\omega Q^{{\delta}-s} \overline{G({\delta}-\bar{s})},
\end{equation}for some δ > 0, with
 $F(s)= \phi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$,
$F(s)= \phi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$,  $G(s) = \psi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$,
$G(s) = \psi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$,  $r\in \mathbb{N}$,
$r\in \mathbb{N}$,  $ \alpha_i \gt 0$,
$ \alpha_i \gt 0$,  $\beta_i \in \mathbb C$ with
$\beta_i \in \mathbb C$ with  $\operatorname{Re} (\beta_i)\geq 0$, Q > 0 and
$\operatorname{Re} (\beta_i)\geq 0$, Q > 0 and  $\omega \in \mathbb C$ with
$\omega \in \mathbb C$ with  $|\omega|=1$. More precisely, this means that there exists a domain D which is the exterior of a compact set S, such that in D, there is an analytic function
$|\omega|=1$. More precisely, this means that there exists a domain D which is the exterior of a compact set S, such that in D, there is an analytic function  $\chi(s)$ with the properties:
$\chi(s)$ with the properties:(i)
 $\chi(s)= Q^sF(s)$ for
$\chi(s)= Q^sF(s)$ for  $\operatorname{Re}(s) \gt \sigma_a$ and
$\operatorname{Re}(s) \gt \sigma_a$ and  $\chi(s)= \omega Q^{{\delta}-s} \overline{G({\delta}-\bar{s})}$ for
$\chi(s)= \omega Q^{{\delta}-s} \overline{G({\delta}-\bar{s})}$ for  $\operatorname{Re}(s) \lt \delta-\sigma_b$.
$\operatorname{Re}(s) \lt \delta-\sigma_b$.(ii) For some constant θ < 1,
(1.7) \begin{equation}
\chi(s)=O\left(\exp\left[\exp\left(\frac{\theta \pi|s|}{{\sigma}_2-{\sigma}_1}\right)\right]\right),
\end{equation}
\begin{equation}
\chi(s)=O\left(\exp\left[\exp\left(\frac{\theta \pi|s|}{{\sigma}_2-{\sigma}_1}\right)\right]\right),
\end{equation}uniformly in every strip
 $-\infty \lt \sigma_1\leq \operatorname{Re}(s) \leq \sigma_2 \lt \infty$.
$-\infty \lt \sigma_1\leq \operatorname{Re}(s) \leq \sigma_2 \lt \infty$.
Given the functional equation (1.6), we define the vectors ![]() $\boldsymbol \alpha,\, \boldsymbol \beta$ and the quantity dF by
$\boldsymbol \alpha,\, \boldsymbol \beta$ and the quantity dF by ![]() $\boldsymbol \alpha =(\alpha_1, \ldots, \alpha_r),\, \boldsymbol \beta=(\beta_1, \ldots, \beta_r)$, and
$\boldsymbol \alpha =(\alpha_1, \ldots, \alpha_r),\, \boldsymbol \beta=(\beta_1, \ldots, \beta_r)$, and ![]() $d_F=2\sum_{i=1}^{r}\alpha_i$. We will also denote the vector
$d_F=2\sum_{i=1}^{r}\alpha_i$. We will also denote the vector ![]() $(\bar{\beta}_1, \ldots, \bar{\beta}_r)$ by
$(\bar{\beta}_1, \ldots, \bar{\beta}_r)$ by ![]() $\boldsymbol{\bar{\beta}}$. In the case of functions in the Selberg class, dF is said to be the degree of the function, which acts as an invariant. We will denote
$\boldsymbol{\bar{\beta}}$. In the case of functions in the Selberg class, dF is said to be the degree of the function, which acts as an invariant. We will denote ![]() $\frac{d_F}{2}$ by
$\frac{d_F}{2}$ by ![]() $d_F^{'}$ throughout this article. In [Reference Chandrasekharan and Narasimhan19], Chandrasekharan and Narasimhan considered the same class of Dirichlet series with the stronger restriction:
$d_F^{'}$ throughout this article. In [Reference Chandrasekharan and Narasimhan19], Chandrasekharan and Narasimhan considered the same class of Dirichlet series with the stronger restriction:
 \begin{align}
\lim_{|t|\to\infty}\chi(\sigma+it)=0,
\end{align}
\begin{align}
\lim_{|t|\to\infty}\chi(\sigma+it)=0,
\end{align} uniformly in every bounded strip ![]() $-\infty \lt \sigma_1\leq\sigma\leq\sigma_2 \lt \infty$. In [Reference Chandrasekharan and Narasimhan19], they derived an identity of the type (1.13) and showed that if
$-\infty \lt \sigma_1\leq\sigma\leq\sigma_2 \lt \infty$. In [Reference Chandrasekharan and Narasimhan19], they derived an identity of the type (1.13) and showed that if ![]() $\operatorname{Re} b(n)\neq 0$ for at least one value of n, then
$\operatorname{Re} b(n)\neq 0$ for at least one value of n, then ![]() $ \operatorname{Re}[S_{\rho}(x)-Q_{\rho}(x)]= \Omega_{\pm}\left(x^{\theta}\right),$ where Sρ and Qρ are as in (1.21) and (1.22), respectively, and
$ \operatorname{Re}[S_{\rho}(x)-Q_{\rho}(x)]= \Omega_{\pm}\left(x^{\theta}\right),$ where Sρ and Qρ are as in (1.21) and (1.22), respectively, and  $\theta=\frac{1}{d_F}\left(d_F^{'}\delta+\rho(d_F-1)-1/2\right)$.
$\theta=\frac{1}{d_F}\left(d_F^{'}\delta+\rho(d_F-1)-1/2\right)$.
The following two theorems are concerned with the equivalence of the functional equation and the modular relation for our class of Dirichlet series ![]() $\mathcal C$. Such equivalences have been proved by Bochner [Reference Bochner13] and Kanemitsu, Tanigawa, Tsukada [Reference Kanemitsu, Tanigawa and Tsukada30]. Results proving the modular relation from the functional equation have also been given by Tsukada [Reference Tsukada39] and Kanemitsu, Tanigawa, Tsukada [Reference Kanemitsu, Tanigawa and Tsukada29]. From each of these works, one can derive the corresponding result for a subset of functions in the class
$\mathcal C$. Such equivalences have been proved by Bochner [Reference Bochner13] and Kanemitsu, Tanigawa, Tsukada [Reference Kanemitsu, Tanigawa and Tsukada30]. Results proving the modular relation from the functional equation have also been given by Tsukada [Reference Tsukada39] and Kanemitsu, Tanigawa, Tsukada [Reference Kanemitsu, Tanigawa and Tsukada29]. From each of these works, one can derive the corresponding result for a subset of functions in the class ![]() $\mathcal{C}$, namely those for which χ from definition 1.1 satisfies the stricter restriction (1.8). In theorems 1.2 and 1.3, we prove the equivalence of the functional equation and the modular relation for the entire class
$\mathcal{C}$, namely those for which χ from definition 1.1 satisfies the stricter restriction (1.8). In theorems 1.2 and 1.3, we prove the equivalence of the functional equation and the modular relation for the entire class ![]() $\mathcal C$. In particular, we consider the more relaxed growth condition (1.7) on χ.
$\mathcal C$. In particular, we consider the more relaxed growth condition (1.7) on χ.
Theorem 1.2 Let ![]() $\phi(s)$ and
$\phi(s)$ and ![]() $\psi(s)$ be two Dirichlet series in the class
$\psi(s)$ be two Dirichlet series in the class ![]() $\mathcal{C}$. Then the functional equation
$\mathcal{C}$. Then the functional equation
where ![]() $F(s)= \phi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$,
$F(s)= \phi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$, ![]() $G(s) = \psi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$, implies the modular relation
$G(s) = \psi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$, implies the modular relation
 \begin{equation}
\sum_{n=1}^{\infty}a_nZ_{\boldsymbol\alpha, \boldsymbol \beta}(\lambda_nx)=P(x)+\frac{\omega}{(xQ)^\delta}\sum_{n=1}^{\infty}\bar{b}_n Z_{\boldsymbol \alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_n}{Q^2x}\bigg), \ \ (x \gt 0),
\end{equation}
\begin{equation}
\sum_{n=1}^{\infty}a_nZ_{\boldsymbol\alpha, \boldsymbol \beta}(\lambda_nx)=P(x)+\frac{\omega}{(xQ)^\delta}\sum_{n=1}^{\infty}\bar{b}_n Z_{\boldsymbol \alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_n}{Q^2x}\bigg), \ \ (x \gt 0),
\end{equation} where for ![]() $x,a \gt 0$,
$x,a \gt 0$,
 \begin{equation}
Z_{\boldsymbol\alpha,\boldsymbol\beta}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds.
\end{equation}
\begin{equation}
Z_{\boldsymbol\alpha,\boldsymbol\beta}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds.
\end{equation}P(x) is a residual function given by
 \begin{align}
P(x)= \frac{1}{2 \pi i}\int_{C} F(s) x^{-s}ds,
\end{align}
\begin{align}
P(x)= \frac{1}{2 \pi i}\int_{C} F(s) x^{-s}ds,
\end{align}and C denotes a circle of finite radius, lying inside the domain D and containing all the singularities of F(s).
In the next result, we show that the functional equation implies a Riesz-sum identity for series in our class ![]() $\mathcal{C}$, with the smallest possible value of ρ, analogous to the ρ = 0 case in (1.4). Such results were proved by Chandrasekharan and Narasimhan [Reference Chandrasekharan and Narasimhan19, Eq. (1.3)] and Hafner [Reference Hafner43] for Dirichlet series satisfying functional equations with multiple Gamma factors, with the growth condition (1.8) on
$\mathcal{C}$, with the smallest possible value of ρ, analogous to the ρ = 0 case in (1.4). Such results were proved by Chandrasekharan and Narasimhan [Reference Chandrasekharan and Narasimhan19, Eq. (1.3)] and Hafner [Reference Hafner43] for Dirichlet series satisfying functional equations with multiple Gamma factors, with the growth condition (1.8) on ![]() $\chi(s)$. Our result below holds for a larger class of functions, since χ fulfils the more relaxed growth condition (1.7).
$\chi(s)$. Our result below holds for a larger class of functions, since χ fulfils the more relaxed growth condition (1.7).
Theorem 1.4 Let ![]() $\phi(s)$ and
$\phi(s)$ and ![]() $\psi(s)$ be two Dirichlet series satisfying definition 1.1. Let
$\psi(s)$ be two Dirichlet series satisfying definition 1.1. Let ![]() $a \gt \max\{0,{\sigma}_a,{\sigma}_b\}$ be sufficiently large so that all the singularities of
$a \gt \max\{0,{\sigma}_a,{\sigma}_b\}$ be sufficiently large so that all the singularities of ![]() $F(s)= \phi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$ are contained in the strip
$F(s)= \phi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$ are contained in the strip ![]() ${\delta}-a \lt \operatorname{Re}(s) \lt a$. Then the functional equation
${\delta}-a \lt \operatorname{Re}(s) \lt a$. Then the functional equation
where ![]() $G(s) = \psi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$, implies the identity
$G(s) = \psi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$, implies the identity
 \begin{align}
& \frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{\lambda_n \leq x} a_{n}(x-\lambda_n)^\rho \notag\\
& \quad = Q_\rho(x)+\bigg(\frac{\omega x^{\delta+\rho}}{Q^\delta}\bigg) \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \qquad \times \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_i s+\bar{\beta}_i)}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds ,
\end{align}
\begin{align}
& \frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{\lambda_n \leq x} a_{n}(x-\lambda_n)^\rho \notag\\
& \quad = Q_\rho(x)+\bigg(\frac{\omega x^{\delta+\rho}}{Q^\delta}\bigg) \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \qquad \times \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_i s+\bar{\beta}_i)}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds ,
\end{align} for x > 0, and  ${\rho} \gt (2{\sigma}_b-{\delta})d_F^{'}-\frac{1}{2}$. Here,
${\rho} \gt (2{\sigma}_b-{\delta})d_F^{'}-\frac{1}{2}$. Here,  $d_F^{'}=\sum_{i=1}^{r}\alpha_i$ and
$d_F^{'}=\sum_{i=1}^{r}\alpha_i$ and ![]() $Q_\rho(x)$ is a residual function given by
$Q_\rho(x)$ is a residual function given by
 \begin{equation}
Q_\rho(x)=\frac{1}{2 \pi i}\int_{C}\frac{\phi(s)\Gamma(s)x^{s+\rho}}{\Gamma(s+\rho+1)} ds,
\end{equation}
\begin{equation}
Q_\rho(x)=\frac{1}{2 \pi i}\int_{C}\frac{\phi(s)\Gamma(s)x^{s+\rho}}{\Gamma(s+\rho+1)} ds,
\end{equation} where ![]() $C=C_a$ denotes a circle of finite radius, lying inside the strip
$C=C_a$ denotes a circle of finite radius, lying inside the strip ![]() ${\delta}-a \lt \operatorname{Re}(s) \lt a$, containing all the singularities of F(s), such that all the singularities of
${\delta}-a \lt \operatorname{Re}(s) \lt a$, containing all the singularities of F(s), such that all the singularities of ![]() $\phi(s)\Gamma(s)x^{s+\rho}$ which lie in this strip are contained inside C.
$\phi(s)\Gamma(s)x^{s+\rho}$ which lie in this strip are contained inside C.
Remark 1.5. The residual function P(x) given in (1.12) is the sum of residues of ![]() $F(s) x^{-s}$. This function P(x) is independent of the choice of a as long as C contains all the singularities of F(s). On the other hand, the residual function
$F(s) x^{-s}$. This function P(x) is independent of the choice of a as long as C contains all the singularities of F(s). On the other hand, the residual function ![]() $Q_\rho(x)$ given in (1.14) is not invariant of the choice of a as C may not encircle all the poles of the integrand. Since the gamma factor in the numerator of the integrand has infinitely many poles, the number of residues contributed by this factor may vary depending upon a. We also remark that in all our results, C can be taken to be a curve with bounded interior rather than a circle with finite radius.
$Q_\rho(x)$ given in (1.14) is not invariant of the choice of a as C may not encircle all the poles of the integrand. Since the gamma factor in the numerator of the integrand has infinitely many poles, the number of residues contributed by this factor may vary depending upon a. We also remark that in all our results, C can be taken to be a curve with bounded interior rather than a circle with finite radius.
Remark 1.6. Although (1.13) does not appear to be a closed form, one actually has an asymptotic formula for the integral on the right-hand side, given by lemma 2.11. This allows one to express the right-hand side in terms of cosine functions. For practical purposes of computation, this is as convenient as having a Voronoï summation formula in terms of Bessel functions.
The main contribution of this article is to show that the Riesz sum identity (1.13) implies the functional equation. Our key idea is to prove this by introducing an auxiliary modular-type relation, different from the known modular relation (1.10). This new modular-type relation is given by
 \begin{equation*} \sum_{n=1}^{\infty}a_nY_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)=P_1(x)+\frac{\omega}{(xQ)^{\delta}}\sum_{n=1}^{\infty}\bar{b}_n X_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_n}{Q^2x}\bigg), \ \ x \gt 0,
\end{equation*}
\begin{equation*} \sum_{n=1}^{\infty}a_nY_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)=P_1(x)+\frac{\omega}{(xQ)^{\delta}}\sum_{n=1}^{\infty}\bar{b}_n X_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_n}{Q^2x}\bigg), \ \ x \gt 0,
\end{equation*} where ![]() $P_1(x)$ is a residual function which will be defined precisely later,
$P_1(x)$ is a residual function which will be defined precisely later,
 \begin{equation}
Y_{\boldsymbol \alpha,\boldsymbol\beta}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(s)\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds,
\qquad (x,a \gt 0)
\end{equation}
\begin{equation}
Y_{\boldsymbol \alpha,\boldsymbol\beta}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(s)\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds,
\qquad (x,a \gt 0)
\end{equation}and
 \begin{equation}
X_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(\delta-s)\prod_{i=1}^{r} \Gamma(\alpha_i s+ \bar{\beta_i}) x^{-s}ds,
\qquad (x,a \gt 0).
\end{equation}
\begin{equation}
X_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(\delta-s)\prod_{i=1}^{r} \Gamma(\alpha_i s+ \bar{\beta_i}) x^{-s}ds,
\qquad (x,a \gt 0).
\end{equation}It is this auxiliary modular-type relation which acts as an intermediate, allowing us to move from the Riesz sum identity (1.13) to the functional equation (1.9). In the following theorem, we first derive this new modular-type relation from the Riesz sum identity. Subsequently, we will deduce the functional equation (1.9) from this using similar techniques as in the proof of theorem 1.3.
Theorem 1.7 Let ![]() $a \gt \max\{0,{\sigma}_a,{\sigma}_b\}$ be sufficiently large so that all the singularities of
$a \gt \max\{0,{\sigma}_a,{\sigma}_b\}$ be sufficiently large so that all the singularities of ![]() $F(s)= \phi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$ are contained in the strip
$F(s)= \phi(s)\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)$ are contained in the strip ![]() ${\delta}-a \lt \operatorname{Re}(s) \lt a$. Let
${\delta}-a \lt \operatorname{Re}(s) \lt a$. Let ![]() $C=C_a$ be a curve as in the statement of theorem 1.4. Then, the Riesz sum identity (1.13) implies the modular relation
$C=C_a$ be a curve as in the statement of theorem 1.4. Then, the Riesz sum identity (1.13) implies the modular relation
 \begin{equation}
\sum_{n=1}^{\infty}a_nY_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)=P_1(x)+\frac{\omega}{(xQ)^{\delta}}\sum_{n=1}^{\infty}\bar{b}_n X_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_n}{Q^2x}\bigg), \ \ x \gt 0,
\end{equation}
\begin{equation}
\sum_{n=1}^{\infty}a_nY_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)=P_1(x)+\frac{\omega}{(xQ)^{\delta}}\sum_{n=1}^{\infty}\bar{b}_n X_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_n}{Q^2x}\bigg), \ \ x \gt 0,
\end{equation} where ![]() $Y_{\boldsymbol \alpha,\boldsymbol\beta}(x)$ and
$Y_{\boldsymbol \alpha,\boldsymbol\beta}(x)$ and ![]() $X_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}(x)$ are as defined as in (1.15) and (1.16) respectively and
$X_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}(x)$ are as defined as in (1.15) and (1.16) respectively and ![]() $P_1(x)$ is a residual function given by
$P_1(x)$ is a residual function given by
 \begin{equation*}
P_1(x)= \frac{1}{2 \pi i}\int_{C} \Gamma(s) F(s) x^{-s}ds.
\end{equation*}
\begin{equation*}
P_1(x)= \frac{1}{2 \pi i}\int_{C} \Gamma(s) F(s) x^{-s}ds.
\end{equation*}In the following theorem, we show that the functional equation (1.9) can be obtained from this auxiliary modular relation (1.17).
The following corollary follows from theorems 1.2, 1.3, 1.4, 1.7, and 1.8.
Corollary 1.9. The functional equation (1.9), modular relations (1.10) and (1.17), and the Riesz sum identity (1.13) are equivalent.
We now discuss in more detail recent literature related to these results. In [Reference Bochner13], Bochner defined Dirichlet series of Hecke-type as follows. Let λn and µn be two strictly increasing sequences of real numbers tending to ![]() $\infty$ and let
$\infty$ and let ![]() ${a(n)}, {b(n)}$ be two sequences of complex numbers not identically zero. Consider the functions
${a(n)}, {b(n)}$ be two sequences of complex numbers not identically zero. Consider the functions ![]() $\phi(s)$ and
$\phi(s)$ and ![]() $\psi(s)$ representable as Dirichlet series
$\psi(s)$ representable as Dirichlet series
 \begin{equation}
\phi(s)=\sum_{n=1}^{\infty} \frac{a(n)}{\lambda_n^{s}} \ \ \text{and}\,\,\, \psi(s)=\sum_{n=1}^{\infty} \frac{b(n)}{\mu_n^{s}},
\end{equation}
\begin{equation}
\phi(s)=\sum_{n=1}^{\infty} \frac{a(n)}{\lambda_n^{s}} \ \ \text{and}\,\,\, \psi(s)=\sum_{n=1}^{\infty} \frac{b(n)}{\mu_n^{s}},
\end{equation}with finite abscissa of absolute convergence σa and σb respectively.
These Dirichlet series satisfy the functional equation
for some δ > 0. That is, there exists a domain D which is the exterior of a bounded closed set S, such that in D there exists a holomorphic function ![]() $\chi(s)$ satisfying
$\chi(s)$ satisfying
 \begin{align*}
\lim_{|t|\to\infty}\chi(\sigma+it)=0
\end{align*}
\begin{align*}
\lim_{|t|\to\infty}\chi(\sigma+it)=0
\end{align*} uniformly in every bounded strip ![]() $-\infty \lt \sigma_1\leq\sigma\leq\sigma_2 \lt \infty$, with
$-\infty \lt \sigma_1\leq\sigma\leq\sigma_2 \lt \infty$, with ![]() $\chi(s)=(2\pi)^{-s} \Gamma(s)\phi(s)$ for all
$\chi(s)=(2\pi)^{-s} \Gamma(s)\phi(s)$ for all ![]() $\sigma \gt \sigma_a$, and
$\sigma \gt \sigma_a$, and ![]() $\chi(s)=(2\pi)^{s-\delta}\Gamma(\delta-s)\psi(\delta-s)$ for all
$\chi(s)=(2\pi)^{s-\delta}\Gamma(\delta-s)\psi(\delta-s)$ for all ![]() $\sigma \lt {\delta- \sigma_b}$. Bochner proved that the functional equation (1.19) is equivalent to the modular relation
$\sigma \lt {\delta- \sigma_b}$. Bochner proved that the functional equation (1.19) is equivalent to the modular relation
 \begin{align}
\sum_{n=1}^{\infty}a(n)e^{-\lambda_nx}=P(x)+\left(\frac{2\pi}{x}\right)^{\delta} \sum_{n=1}^{\infty}b(n)e^{-4\pi^2\mu_n/x},
\end{align}
\begin{align}
\sum_{n=1}^{\infty}a(n)e^{-\lambda_nx}=P(x)+\left(\frac{2\pi}{x}\right)^{\delta} \sum_{n=1}^{\infty}b(n)e^{-4\pi^2\mu_n/x},
\end{align}where
 \begin{align*}
P(x)=\frac{1}{2\pi i}\int_{C}\chi(s)\left(\frac{2\pi}{x}\right)^s\,ds,
\end{align*}
\begin{align*}
P(x)=\frac{1}{2\pi i}\int_{C}\chi(s)\left(\frac{2\pi}{x}\right)^s\,ds,
\end{align*} and C denotes a curve (or curves) in D containing the set S. Chandrasekharan and Narasimhan [Reference Chandrasekharan and Narasimhan17] considered the same functional equation with arbitrary real δ and a more relaxed growth condition on ![]() $\chi(s)$. In particular, they considered
$\chi(s)$. In particular, they considered
 \begin{align*}
e^{-\epsilon|t|}\chi(\sigma+it)=O(1)
\end{align*}
\begin{align*}
e^{-\epsilon|t|}\chi(\sigma+it)=O(1)
\end{align*} with ![]() $0 \lt \epsilon \lt \pi/2$ as
$0 \lt \epsilon \lt \pi/2$ as ![]() $|t|\to\infty$, uniformly in every bounded strip
$|t|\to\infty$, uniformly in every bounded strip ![]() $-\infty \lt \sigma_1\leq\sigma\leq\sigma_2 \lt \infty$. They proved the equivalence of the functional equation (1.19) and the modular relation (1.20). In the same article, they also considered the identity
$-\infty \lt \sigma_1\leq\sigma\leq\sigma_2 \lt \infty$. They proved the equivalence of the functional equation (1.19) and the modular relation (1.20). In the same article, they also considered the identity
 \begin{align}
S_{\rho}(x) & := \frac{1}{\Gamma(\rho +1)}\sideset{}{'}\sum_{\lambda_n\leq x}a(n)(x-\lambda_n)^{\rho} \notag\\
& =\left(\frac{1}{2\pi}\right)^{\rho}\sum_{n=1}^{\infty}\left(\frac{x}{\mu_n}\right)^{\frac{1}{2}(\delta+\rho)}b(n)J_{\delta+\rho}(4\pi\sqrt{\mu_nx})+Q_{\rho}(x),
\end{align}
\begin{align}
S_{\rho}(x) & := \frac{1}{\Gamma(\rho +1)}\sideset{}{'}\sum_{\lambda_n\leq x}a(n)(x-\lambda_n)^{\rho} \notag\\
& =\left(\frac{1}{2\pi}\right)^{\rho}\sum_{n=1}^{\infty}\left(\frac{x}{\mu_n}\right)^{\frac{1}{2}(\delta+\rho)}b(n)J_{\delta+\rho}(4\pi\sqrt{\mu_nx})+Q_{\rho}(x),
\end{align} where ![]() $J_{{\delta}+{\rho}}$ denotes the Bessel function of the first kind of order
$J_{{\delta}+{\rho}}$ denotes the Bessel function of the first kind of order ![]() ${\delta}+{\rho}$, Qρ is a residual function defined by
${\delta}+{\rho}$, Qρ is a residual function defined by
 \begin{align}
Q_{\rho}(x)=\frac{1}{2\pi i}\int_{C}\frac{\chi(s)(2\pi)^sx^{s+\rho}}{\Gamma(\rho+1+s)}\,ds,
\end{align}
\begin{align}
Q_{\rho}(x)=\frac{1}{2\pi i}\int_{C}\frac{\chi(s)(2\pi)^sx^{s+\rho}}{\Gamma(\rho+1+s)}\,ds,
\end{align} and C denotes a curve (or curves) in D containing the set S. They proved that the identity (1.21) for x > 0 and  $\rho\geq 2\sigma_b-\delta-\frac{1}{2}$ is equivalent to the functional equation (1.19). In [Reference Chandrasekharan and Narasimhan18], the arithmetic identity (1.21) served as the main tool for Chandrasekharan and Narasimhan to obtain the omega-bound
$\rho\geq 2\sigma_b-\delta-\frac{1}{2}$ is equivalent to the functional equation (1.19). In [Reference Chandrasekharan and Narasimhan18], the arithmetic identity (1.21) served as the main tool for Chandrasekharan and Narasimhan to obtain the omega-bound
 \begin{align*}
\operatorname{Re}[S_{\rho}(x)-Q_{\rho}(x)]=\Omega_{\pm}\left(x^{\frac{\delta}{2}+\frac{\rho}{2}-\frac{1}{4}}\right),
\end{align*}
\begin{align*}
\operatorname{Re}[S_{\rho}(x)-Q_{\rho}(x)]=\Omega_{\pm}\left(x^{\frac{\delta}{2}+\frac{\rho}{2}-\frac{1}{4}}\right),
\end{align*} if ![]() $\operatorname{Re} b(n)\neq 0$ for at least one value of n and
$\operatorname{Re} b(n)\neq 0$ for at least one value of n and
 \begin{align*}
\operatorname{Im}[S_{\rho}(x)-Q_{\rho}(x)]=\Omega_{\pm}\left(x^{\frac{\delta}{2}+\frac{\rho}{2}-\frac{1}{4}}\right),
\end{align*}
\begin{align*}
\operatorname{Im}[S_{\rho}(x)-Q_{\rho}(x)]=\Omega_{\pm}\left(x^{\frac{\delta}{2}+\frac{\rho}{2}-\frac{1}{4}}\right),
\end{align*} if ![]() $\operatorname{Im} b(n) \neq 0$ for at least one value of n.
$\operatorname{Im} b(n) \neq 0$ for at least one value of n.
Bochner (p. 341, [Reference Bochner13]) made the following observation about the modular relation (1.20). If the function ![]() $\chi(s)$ has simple poles at s = 0 and
$\chi(s)$ has simple poles at s = 0 and ![]() $s=\delta$ then the residual function P(x) can be written in the form
$s=\delta$ then the residual function P(x) can be written in the form ![]() $-a(0)+b(0)x^{-\delta}$ for some
$-a(0)+b(0)x^{-\delta}$ for some ![]() $a(0), b(0) \in \mathbb{C}$. In this case, the modular relation (1.20) can be re-written as
$a(0), b(0) \in \mathbb{C}$. In this case, the modular relation (1.20) can be re-written as
 \begin{align*} \sum_{n=0}^{\infty}a(n)e^{-\lambda'_nx}={x}^{-\delta} \left( \sum_{n=0}^{\infty}b(n)e^{-\mu'_n/x} \right),
\end{align*}
\begin{align*} \sum_{n=0}^{\infty}a(n)e^{-\lambda'_nx}={x}^{-\delta} \left( \sum_{n=0}^{\infty}b(n)e^{-\mu'_n/x} \right),
\end{align*} where ![]() $\lambda'_n={2\pi} {\lambda_n}$ and
$\lambda'_n={2\pi} {\lambda_n}$ and ![]() $\mu'_n={2\pi}{\mu_n}$ and
$\mu'_n={2\pi}{\mu_n}$ and ![]() $\lambda'_0 =0 =\mu_0'$. This modular relation implies the summation formula
$\lambda'_0 =0 =\mu_0'$. This modular relation implies the summation formula
 \begin{align}
\sum_{n=0}^{\infty}a(n)f(\lambda'_nx)={x}^{-\delta} \sum_{n=0}^{\infty}b(n)g(\mu'_n/x),
\end{align}
\begin{align}
\sum_{n=0}^{\infty}a(n)f(\lambda'_nx)={x}^{-\delta} \sum_{n=0}^{\infty}b(n)g(\mu'_n/x),
\end{align} for some pair of functions ![]() $f,g$ which are connected by the Hankel transformations
$f,g$ which are connected by the Hankel transformations
 \begin{align*}
g(t)=t^{-\frac{1}{2}(\delta-1)}\int_0^{\infty}J_{\delta-1}(2\sqrt{tx})x^{\frac{1}{2}(\delta-1)}f(x)\,dx,
\\ f(x)=x^{-\frac{1}{2}(\delta-1)}\int_0^{\infty}J_{\delta-1}(2\sqrt{tx})t^{\frac{1}{2}(\delta-1)}f(t)\,dt.
\end{align*}
\begin{align*}
g(t)=t^{-\frac{1}{2}(\delta-1)}\int_0^{\infty}J_{\delta-1}(2\sqrt{tx})x^{\frac{1}{2}(\delta-1)}f(x)\,dx,
\\ f(x)=x^{-\frac{1}{2}(\delta-1)}\int_0^{\infty}J_{\delta-1}(2\sqrt{tx})t^{\frac{1}{2}(\delta-1)}f(t)\,dt.
\end{align*} If one chooses x = 1 and the support of f is compact, then (1.23) yields analogues of the Voronoï summation formula (1.3). Moreover, if ![]() $\rho\geq 0$ (for instance if
$\rho\geq 0$ (for instance if  $2\sigma_b\geq \delta+ \frac{1}{2}$) in the identity (1.21), then analogues of the Voronoï summation formula can be obtained for
$2\sigma_b\geq \delta+ \frac{1}{2}$) in the identity (1.21), then analogues of the Voronoï summation formula can be obtained for ![]() $\sum a(n)f(n)$ by an argument similar to that discussed for (1.5).
$\sum a(n)f(n)$ by an argument similar to that discussed for (1.5).
In [Reference Berndt4], Berndt considered the Dirichlet series (1.18) and allowed for higher powers of the Gamma function in the functional equation. More precisely, he defined the holomorphic function ![]() $\chi(s)$ by
$\chi(s)$ by ![]() $\chi(s)= \Gamma^m(s)\phi(s)$ for all
$\chi(s)= \Gamma^m(s)\phi(s)$ for all ![]() $\sigma \gt \sigma_a$ and
$\sigma \gt \sigma_a$ and ![]() $\chi(s)=\Gamma^m(\delta-s)\psi(\delta-s)$ for all
$\chi(s)=\Gamma^m(\delta-s)\psi(\delta-s)$ for all ![]() $\sigma \lt \delta-\sigma_b$. Let p be the smallest positive integer so that
$\sigma \lt \delta-\sigma_b$. Let p be the smallest positive integer so that  $\gamma= \sigma_b+p-\frac{1}{4m} \gt \max(0,\sigma_a,\sigma_b)$. Berndt showed that if
$\gamma= \sigma_b+p-\frac{1}{4m} \gt \max(0,\sigma_a,\sigma_b)$. Berndt showed that if
 \begin{align*}
\chi(s)=O\left(e^{\exp\left(\frac{\theta \pi |s|}{2\gamma-{\delta}}\right)}\right),
\end{align*}
\begin{align*}
\chi(s)=O\left(e^{\exp\left(\frac{\theta \pi |s|}{2\gamma-{\delta}}\right)}\right),
\end{align*} for some θ < 1, uniformly in the half-strip ![]() $\delta-\gamma \lt \sigma \lt \gamma$,
$\delta-\gamma \lt \sigma \lt \gamma$, ![]() $|t|\geq \eta$ contained in D, then we have an equivalence between the functional equation
$|t|\geq \eta$ contained in D, then we have an equivalence between the functional equation ![]() $\chi(s)=\chi({\delta}-s)$ and the identities
$\chi(s)=\chi({\delta}-s)$ and the identities
 \begin{align}
\sum_{n=1}^{\infty}a(n)E_m(\lambda_nx)=P(x)+x^{-\delta} \sum_{n=1}^{\infty}b(n)E_m(\mu_n/x),
\quad (x \gt 0)
\end{align}
\begin{align}
\sum_{n=1}^{\infty}a(n)E_m(\lambda_nx)=P(x)+x^{-\delta} \sum_{n=1}^{\infty}b(n)E_m(\mu_n/x),
\quad (x \gt 0)
\end{align}and
 \begin{align*}
& \frac{1}{\Gamma(\rho +1)}\sideset{}{'}\sum_{\lambda_n\leq x}a(n)(x-\lambda_n)^{\rho}\notag\\
& =2^{\rho(1-m)}\sum_{n=1}^{\infty}\left(\frac{x}{\mu_n}\right)^{\frac{1}{2}(\delta+\rho)}b(n)K_{\delta+\rho}(2^m\sqrt{\mu_nx}; {\delta}-1; m)+Q_{\rho}(x),
\end{align*}
\begin{align*}
& \frac{1}{\Gamma(\rho +1)}\sideset{}{'}\sum_{\lambda_n\leq x}a(n)(x-\lambda_n)^{\rho}\notag\\
& =2^{\rho(1-m)}\sum_{n=1}^{\infty}\left(\frac{x}{\mu_n}\right)^{\frac{1}{2}(\delta+\rho)}b(n)K_{\delta+\rho}(2^m\sqrt{\mu_nx}; {\delta}-1; m)+Q_{\rho}(x),
\end{align*} for ![]() $\delta \gt -1/2$ and
$\delta \gt -1/2$ and ![]() $\rho \gt 2m\sigma_b-m\delta-1/2$. Here
$\rho \gt 2m\sigma_b-m\delta-1/2$. Here
 \begin{align*}
E_m(x)=\frac{1}{2\pi i}\int_{(c)}\Gamma^m(s)x^{-s}\,ds, \quad c \gt 0, x \gt 0,
\end{align*}
\begin{align*}
E_m(x)=\frac{1}{2\pi i}\int_{(c)}\Gamma^m(s)x^{-s}\,ds, \quad c \gt 0, x \gt 0,
\end{align*} \begin{align*}
K_{\nu}(x;\mu;m)=\frac{1}{2\pi i } \int_{(c)}\frac{2^{2ms-(m-1)\mu-\nu-m+1}\Gamma(s)x^{\nu-2s}}{\Gamma^{m-1}(\mu+1-s)\Gamma(\nu+1-s)}\,ds,\quad 0 \lt c \lt \frac{1}{2}\min (\mu,\nu)+\frac{3}{4},
\end{align*}
\begin{align*}
K_{\nu}(x;\mu;m)=\frac{1}{2\pi i } \int_{(c)}\frac{2^{2ms-(m-1)\mu-\nu-m+1}\Gamma(s)x^{\nu-2s}}{\Gamma^{m-1}(\mu+1-s)\Gamma(\nu+1-s)}\,ds,\quad 0 \lt c \lt \frac{1}{2}\min (\mu,\nu)+\frac{3}{4},
\end{align*} \begin{align*}
P(x)=\frac{1}{2\pi i}\int_{C}\chi(s)x^{-s}\,ds
\ \text{and }
Q_{\rho}(x)=\frac{1}{2\pi i}\int_{C}\frac{\Gamma(s)\phi(s)x^{s+\rho}}{\Gamma(\rho+1+s)}\,ds,
\end{align*}
\begin{align*}
P(x)=\frac{1}{2\pi i}\int_{C}\chi(s)x^{-s}\,ds
\ \text{and }
Q_{\rho}(x)=\frac{1}{2\pi i}\int_{C}\frac{\Gamma(s)\phi(s)x^{s+\rho}}{\Gamma(\rho+1+s)}\,ds,
\end{align*}where C denotes a curve (or curves) in D containing the set S.
In a series of articles, Berndt [Reference Berndt3, Reference Berndt5–Reference Berndt8] presented a detailed study of Riesz-type summation formulae for various classes of Dirichlet series. In [Reference Berndt, Kim and Zaharescu12], Berndt, Kim, and Zaharescu studied various Riesz-type sums and then in [Reference Kim32], Kim gave Riesz-type identities for weighted sums of divisor functions. In recent work by Berndt, Dixit, Gupta, and Zaharescu [Reference Berndt, Dixit, Gupta and Zaharescu9, Reference Berndt, Dixit, Gupta and Zaharescu10], they obtained new identities of the type (1.21) involving the modified Bessel function ![]() $K_{\nu}(z)$ of order ν.
$K_{\nu}(z)$ of order ν.
In [Reference Berndt, Dixit, Roy and Zaharescu11, theorem 6.1], the first author along with Berndt, Dixit, and Zaharescu proved a Voronoï summation formula analogous to (1.2) for the divisor function ![]() $\sigma_s(n)$. Subsequently, Dixit, Maji, and Vatwani [Reference Dixit, Maji and Vatwani21, theorem 2.2] obtained a version of the Voronoï summation formula for a more general divisor function
$\sigma_s(n)$. Subsequently, Dixit, Maji, and Vatwani [Reference Dixit, Maji and Vatwani21, theorem 2.2] obtained a version of the Voronoï summation formula for a more general divisor function  $\sigma_s^{(k)}(n)$, which gives [Reference Berndt, Dixit, Roy and Zaharescu11, theorem 6.1] as a corollary but for a larger domain. Again in [Reference Banerjee and Maji2], Banerjee and Maji obtained a summation formula for
$\sigma_s^{(k)}(n)$, which gives [Reference Berndt, Dixit, Roy and Zaharescu11, theorem 6.1] as a corollary but for a larger domain. Again in [Reference Banerjee and Maji2], Banerjee and Maji obtained a summation formula for  $\sigma_s^{(k)}(n)$ involving the modified Bessel function of the second kind.
$\sigma_s^{(k)}(n)$ involving the modified Bessel function of the second kind.
In the literature, there are many studies relevant to obtaining the modular-type relation (1.20) from the functional equation in various settings. For instance, Arai, Chakraborty, Kanemitsu [Reference Arai, Chakraborty and Kanemitsu1] and Chakraborty, Kanemitsu, Maji [Reference Chakraborty, Kanemitsu and Maji15] obtained modular-type relations associated to Dedekind zeta functions and the Rankin–Selberg L-function respectively. A breakthrough result of Tsukada [Reference Tsukada39] gives a more generalized modular-type identity for a class of Dirichlet series. This general result allows one to recover many existing modular-type identities as special cases, for instance (1.20) and (1.24). Further in [Reference Kanemitsu, Tanigawa and Tsukada29, Reference Kanemitsu, Tanigawa and Tsukada30], Kanemitsu, Tanigawa, and Tsukada studied these kinds of generalized modular relations along with many number theoretic applications. In [Reference Kanemitsu, Tanigawa and Tsukada30], they established the equivalence between the functional equation and modular relation in a very general setting. For a more detailed description of these generalized modular relations, we refer the reader to the book [Reference Kanemitsu and Tsukada31] by Kanemitsu and Tsukada.
2. Prerequisites
We define a residual function as done by Bochner in [Reference Bochner13].
Definition 2.1. [Reference Bochner13, definition 2]
A function P(x) is said to be a residual function if
(i) P(x) is defined and differentiable in
 $(0, \infty)$. Moreover,
$(0, \infty)$. Moreover,  $P(x)=O(x^{-c})$ as
$P(x)=O(x^{-c})$ as  $x \rightarrow 0$ and
$x \rightarrow 0$ and  $P(x)=O(x^{c})$ as
$P(x)=O(x^{c})$ as  $x \rightarrow \infty$, for some constant c > 0, so that the functions
$x \rightarrow \infty$, for some constant c > 0, so that the functions
 \begin{equation*}
I_1(s)= \int_{0}^{1} P(x)x^{s-1}dx, \ \ \ \ I_2(s)=- \int_{1}^{\infty} P(x)x^{s-1}dx,
\end{equation*}
\begin{equation*}
I_1(s)= \int_{0}^{1} P(x)x^{s-1}dx, \ \ \ \ I_2(s)=- \int_{1}^{\infty} P(x)x^{s-1}dx,
\end{equation*}can be introduced in some right half-plane and left half-plane respectively.
(ii)
 $I_1(s)$ and
$I_1(s)$ and  $I_2(s)$ can be continued into each other in a domain D as introduced in definition 1.1.
$I_2(s)$ can be continued into each other in a domain D as introduced in definition 1.1.(iii)
 $\lim_{|t|\rightarrow \infty}I(\sigma+it)=0$, uniformly in
$\lim_{|t|\rightarrow \infty}I(\sigma+it)=0$, uniformly in  $-\infty \lt \sigma_1 \leq\sigma\leq\sigma_2 \lt +\infty$, where I denotes the function obtained by analytic continuation in (ii).
$-\infty \lt \sigma_1 \leq\sigma\leq\sigma_2 \lt +\infty$, where I denotes the function obtained by analytic continuation in (ii).
The following example of a residual function was given by Bochner [Reference Bochner13].
Lemma 2.2. [Reference Bochner13, lemma 1]
Suppose ![]() $\chi(s)$ is analytic in a domain D in
$\chi(s)$ is analytic in a domain D in ![]() $\mathbb C$. Then the integral
$\mathbb C$. Then the integral
 \begin{equation*}
P(x)= \frac{1}{2 \pi i}\int_{C} \chi(s)x^{-s}ds,
\end{equation*}
\begin{equation*}
P(x)= \frac{1}{2 \pi i}\int_{C} \chi(s)x^{-s}ds,
\end{equation*} over a bounded curve or curves C in D, with ![]() $x^{-s}=\exp(-s\log x)$,
is a residual function.
$x^{-s}=\exp(-s\log x)$,
is a residual function.
We will need the following information about the integral ![]() $Q_\rho(x)$.
$Q_\rho(x)$.
Lemma 2.3. The residual function ![]() $Q_{\rho}(x)$, defined in (1.14) is a
$Q_{\rho}(x)$, defined in (1.14) is a ![]() $C^{\infty}$ function.
$C^{\infty}$ function.
Proof. As C is a bounded curve or a finite union of bounded curves, it contains a finite number of poles of the integrand. By the Cauchy residue theorem, ![]() $Q_{\rho}(x)$ is the sum of residues at these singularities and is thus a function of the form
$Q_{\rho}(x)$ is the sum of residues at these singularities and is thus a function of the form ![]() $\sum c_\alpha x^{\alpha}$. Since this a finite sum,
$\sum c_\alpha x^{\alpha}$. Since this a finite sum, ![]() $Q_{\rho}(x)$ is a
$Q_{\rho}(x)$ is a ![]() $C^{\infty}$ function, as needed.
$C^{\infty}$ function, as needed.
The following lemma is a version of the Phragmén–Lindelöf principle due to Littlewood [Reference Littlewood33]. We state the version given by Chandrasekharan and Narasimhan [Reference Chandrasekharan and Narasimhan17].
Lemma 2.4. [Reference Chandrasekharan and Narasimhan17, lemma 2]
Suppose that f(s), ![]() $s=\sigma+it$, is regular in a half-strip S defined by
$s=\sigma+it$, is regular in a half-strip S defined by ![]() $a \lt {\sigma} \lt b$,
$a \lt {\sigma} \lt b$, ![]() $|t| \gt c$ and continuous on the boundary. Moreover, if we have
$|t| \gt c$ and continuous on the boundary. Moreover, if we have
 \begin{equation*}
f(s)=O\left(\exp\left[\exp\left(\frac{\theta \pi|s|}{b-a}\right)\right]\right),
\end{equation*}
\begin{equation*}
f(s)=O\left(\exp\left[\exp\left(\frac{\theta \pi|s|}{b-a}\right)\right]\right),
\end{equation*} uniformly in S for θ < 1, and ![]() $f=o(1)$ on x = a, and on x = b, then
$f=o(1)$ on x = a, and on x = b, then ![]() $f=o(1)$ uniformly in S.
$f=o(1)$ uniformly in S.
The gamma function is the Mellin transform of e −x, defined for any ![]() $s \in \mathbb{C} $ with
$s \in \mathbb{C} $ with ![]() $\operatorname{Re}(s) \gt 0$ by the real integral
$\operatorname{Re}(s) \gt 0$ by the real integral
 \begin{equation*} \Gamma (s) = \int_{0}^{\infty} x^{s-1} e^{-x} dx. \end{equation*}
\begin{equation*} \Gamma (s) = \int_{0}^{\infty} x^{s-1} e^{-x} dx. \end{equation*} Similarly, for any ![]() $\alpha, \beta \in \mathbb C$ with
$\alpha, \beta \in \mathbb C$ with ![]() $\operatorname{Re}(\alpha s+\beta) \gt 0$, we can express
$\operatorname{Re}(\alpha s+\beta) \gt 0$, we can express ![]() $\Gamma(\alpha s+\beta)$ as
$\Gamma(\alpha s+\beta)$ as
 \begin{equation}
\Gamma(\alpha s+\beta)=\int_{0}^{\infty} f_{\alpha, \beta}(x) x^{s-1} dx,
\end{equation}
\begin{equation}
\Gamma(\alpha s+\beta)=\int_{0}^{\infty} f_{\alpha, \beta}(x) x^{s-1} dx,
\end{equation}where
 \begin{align}
f_{\alpha, \beta}(x)= \frac{\exp(-x^{1/\alpha})}{\alpha x^{\beta/\alpha}}.
\end{align}
\begin{align}
f_{\alpha, \beta}(x)= \frac{\exp(-x^{1/\alpha})}{\alpha x^{\beta/\alpha}}.
\end{align}We can extend this to a product of gamma functions, for instance, as in Berndt [Reference Berndt4, lemma 5].
Lemma 2.5. Define for ![]() $x, a \gt 0$,
$x, a \gt 0$,
 \begin{equation*}
Y_{\boldsymbol \alpha,\boldsymbol\beta}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(s)\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds,
\end{equation*}
\begin{equation*}
Y_{\boldsymbol \alpha,\boldsymbol\beta}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(s)\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds,
\end{equation*} where ![]() $\boldsymbol \alpha =(\alpha_1, \dots, \alpha_r),\, \boldsymbol \beta=(\beta_1, \dots, \beta_r)$. Then we have,
$\boldsymbol \alpha =(\alpha_1, \dots, \alpha_r),\, \boldsymbol \beta=(\beta_1, \dots, \beta_r)$. Then we have,
 \begin{equation*}
Y_{\boldsymbol \alpha,\boldsymbol\beta}(x)=\int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) \frac{du_r}{u_r} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) \exp\left(\frac{-x}{u_1\cdots u_r}\right) \frac{du_1}{u_1},
\end{equation*}
\begin{equation*}
Y_{\boldsymbol \alpha,\boldsymbol\beta}(x)=\int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) \frac{du_r}{u_r} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) \exp\left(\frac{-x}{u_1\cdots u_r}\right) \frac{du_1}{u_1},
\end{equation*} where ![]() $f_{\alpha,\beta}(x)$ is as defined in (2.2).
$f_{\alpha,\beta}(x)$ is as defined in (2.2).
Proof. We recall the following result on multiple Mellin integrals [Reference Titchmarsh38, p. 53]. If F(s), ![]() $F_1(s)$, …, and
$F_1(s)$, …, and ![]() $F_n(s)$ are Mellin transforms of f(x),
$F_n(s)$ are Mellin transforms of f(x), ![]() $f_1(x)$, …, and
$f_1(x)$, …, and ![]() $f_n(x)$ respectively then
$f_n(x)$ respectively then
 \begin{align*}
&\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}F(s)F_1(s)\cdots F_n(s) x^{-s}ds \\
& \quad =\int_{0}^{\infty}f_n(u_n) \frac{du_n}{u_n} \cdots \int_{0}^{\infty}f_1(u_1) f\left(\frac{x}{u_1\cdots u_n}\right) \frac{du_1}{u_1}.
\end{align*}
\begin{align*}
&\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}F(s)F_1(s)\cdots F_n(s) x^{-s}ds \\
& \quad =\int_{0}^{\infty}f_n(u_n) \frac{du_n}{u_n} \cdots \int_{0}^{\infty}f_1(u_1) f\left(\frac{x}{u_1\cdots u_n}\right) \frac{du_1}{u_1}.
\end{align*}Combining this with (2.1) completes the proof.
We recall an integral transformation formula given by Chandrasekharan and Narasimhan on p. 35 of [Reference Chandrasekharan and Narasimhan20].
Lemma 2.6. For any  $c \lt -\frac{1}{2}, c\notin \mathbb{Z}$ and
$c \lt -\frac{1}{2}, c\notin \mathbb{Z}$ and ![]() $\alpha \in \mathbb{R}$, we have
$\alpha \in \mathbb{R}$, we have
 \begin{equation*}
\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}\Gamma(s)\cos\left(\frac{\pi}{2}s+\alpha \right)x^{-s}ds=\cos(x+\alpha)-\sum_{0\leq n \lt |c|} (-1)^n \frac{x^n}{n!}\cos\left(\alpha-\frac{\pi}{2}n \right).
\end{equation*}
\begin{equation*}
\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}\Gamma(s)\cos\left(\frac{\pi}{2}s+\alpha \right)x^{-s}ds=\cos(x+\alpha)-\sum_{0\leq n \lt |c|} (-1)^n \frac{x^n}{n!}\cos\left(\alpha-\frac{\pi}{2}n \right).
\end{equation*} We will record here a version of Stirling’s asymptotic formula for ![]() $\log{\Gamma(s)}$ (refer to the equation following (8) in [Reference Chandrasekharan and Narasimhan20]).
$\log{\Gamma(s)}$ (refer to the equation following (8) in [Reference Chandrasekharan and Narasimhan20]).
Lemma 2.7. For any ![]() $c\in \mathbb{C}, |\arg s| \lt \pi$, we have as
$c\in \mathbb{C}, |\arg s| \lt \pi$, we have as ![]() $|s|\to \infty$,
$|s|\to \infty$,
 \begin{equation*}
\log \Gamma(s+c)=
\left(s+c- \frac{1}{2}\right)\log s-s+ \frac{\log{2\pi}}{2}+ \sum_{n=1}^{m}C_n s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right),
\end{equation*}
\begin{equation*}
\log \Gamma(s+c)=
\left(s+c- \frac{1}{2}\right)\log s-s+ \frac{\log{2\pi}}{2}+ \sum_{n=1}^{m}C_n s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right),
\end{equation*}where m is any positive integer and Cn are some constants depending on c.
Note that for ![]() $s=\sigma+it$, if σ is fixed and
$s=\sigma+it$, if σ is fixed and
![]() $|t|\rightarrow \infty$, this yields
$|t|\rightarrow \infty$, this yields
 \begin{equation}
|\Gamma(s)|\sim e^{- \frac{\pi}{2}|t|}|t|^{\sigma-\frac{1}{2}}\sqrt{2\pi}.
\end{equation}
\begin{equation}
|\Gamma(s)|\sim e^{- \frac{\pi}{2}|t|}|t|^{\sigma-\frac{1}{2}}\sqrt{2\pi}.
\end{equation}The following lemma is a form of Perron’s formula, given by Chandrasekharan and Minakshisundaram [Reference Chandrasekharan and Minakshisundaram16].
Lemma 2.8. [Reference Chandrasekharan and Minakshisundaram16, lemma 3.65]
If ![]() $f(s)=\sum_{n=1}^{\infty}a_n \lambda_n^{-s}$, with
$f(s)=\sum_{n=1}^{\infty}a_n \lambda_n^{-s}$, with ![]() $\sum_{n=1}^{\infty}|a_n| \lambda_n^{-\alpha} \lt \infty$, then for
$\sum_{n=1}^{\infty}|a_n| \lambda_n^{-\alpha} \lt \infty$, then for ![]() ${\rho} \geq 0$, σ > 0, and
${\rho} \geq 0$, σ > 0, and ![]() $\sigma\geq \alpha$, we have
$\sigma\geq \alpha$, we have
 \begin{equation*}\frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{\lambda_n \leqslant x}{} a_{n}(x-\lambda_n)^\rho=\frac{1}{2\pi i} \int_{\sigma-i \infty}^{\sigma+i \infty} \frac{f(s)\Gamma(s) x^{s+\rho}}{\Gamma(s+\rho+1)}ds,\end{equation*}
\begin{equation*}\frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{\lambda_n \leqslant x}{} a_{n}(x-\lambda_n)^\rho=\frac{1}{2\pi i} \int_{\sigma-i \infty}^{\sigma+i \infty} \frac{f(s)\Gamma(s) x^{s+\rho}}{\Gamma(s+\rho+1)}ds,\end{equation*} the dash indicating that the last term of the sum has to be multiplied by ![]() $\frac{1}{2}$ if ρ = 0 and
$\frac{1}{2}$ if ρ = 0 and ![]() $x=\lambda_n$.
$x=\lambda_n$.
In the following lemma, we provide a growth estimate for ![]() $Z_{\boldsymbol \alpha,\boldsymbol\beta}(x)$, defined in (1.11).
$Z_{\boldsymbol \alpha,\boldsymbol\beta}(x)$, defined in (1.11).
Lemma 2.9. For x > 0, we have
 \begin{equation*}
Z_{\boldsymbol \alpha,\boldsymbol\beta}(x)\ll \exp{\left(-cx^{\frac{1}{d_F^{'}}}\right)},
\end{equation*}
\begin{equation*}
Z_{\boldsymbol \alpha,\boldsymbol\beta}(x)\ll \exp{\left(-cx^{\frac{1}{d_F^{'}}}\right)},
\end{equation*} as ![]() $x\rightarrow \infty $, where c > 0 is a constant depending on α and β, and
$x\rightarrow \infty $, where c > 0 is a constant depending on α and β, and  $d_F^{'}=\sum_{i=1}^{r}\alpha_i$.
$d_F^{'}=\sum_{i=1}^{r}\alpha_i$.
Proof. For some sufficiently large T > 0, let us write
 \begin{align*}
& \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds\\
& \quad =\frac{1}{2 \pi i}\left[\int_{a-i\infty}^{a-iT}+\int_{a-iT}^{a+iT}+\int_{a+iT}^{a+i\infty}\right]\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds \nonumber \\
& \quad =\frac{1}{2 \pi i}\left[I_1+I_2+I_3\right], \qquad (\text{say}).\nonumber
\end{align*}
\begin{align*}
& \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds\\
& \quad =\frac{1}{2 \pi i}\left[\int_{a-i\infty}^{a-iT}+\int_{a-iT}^{a+iT}+\int_{a+iT}^{a+i\infty}\right]\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds \nonumber \\
& \quad =\frac{1}{2 \pi i}\left[I_1+I_2+I_3\right], \qquad (\text{say}).\nonumber
\end{align*} Now take N > a and consider a rectangle R with vertices ![]() $a\pm iT$ and
$a\pm iT$ and ![]() $N\pm iT$. We shall choose N sufficiently large later, depending upon x. For
$N\pm iT$. We shall choose N sufficiently large later, depending upon x. For ![]() $\operatorname{Re}(s) \geq a$, as
$\operatorname{Re}(s) \geq a$, as ![]() $\operatorname{Re}(\alpha_i s+ \beta_i) \gt 0$ for each i, the gamma factors
$\operatorname{Re}(\alpha_i s+ \beta_i) \gt 0$ for each i, the gamma factors ![]() $\Gamma(\alpha_i s+ \beta_i)$ have no singularities inside the rectangle R, so the integrand is analytic inside R. By Cauchy’s residue theorem, we have
$\Gamma(\alpha_i s+ \beta_i)$ have no singularities inside the rectangle R, so the integrand is analytic inside R. By Cauchy’s residue theorem, we have
 \begin{align*}
I_2& =\int_{a-iT}^{a+iT}\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds\\
&= \left[\int_{a-iT}^{N-iT}+\int_{N-iT}^{N+iT}+\int_{N+iT}^{a+iT}\right]\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds
\nonumber \\
&=I_{21}+I_{22}+I_{23}, \qquad (\text{say}).\nonumber
\end{align*}
\begin{align*}
I_2& =\int_{a-iT}^{a+iT}\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds\\
&= \left[\int_{a-iT}^{N-iT}+\int_{N-iT}^{N+iT}+\int_{N+iT}^{a+iT}\right]\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds
\nonumber \\
&=I_{21}+I_{22}+I_{23}, \qquad (\text{say}).\nonumber
\end{align*} We will first estimate I 22 using estimates for the growth of the gamma function. Writing ![]() $s={\sigma}+it$, from lemma 2.7, we have
$s={\sigma}+it$, from lemma 2.7, we have
 \begin{equation}
|\Gamma({\sigma}+it)|\ll e^{-{\sigma}}\left|s^{s-\frac{1}{2}}\right|=e^{-{\sigma}} |s|^{{\sigma}-\frac{1}{2}}e^{-t\arg s},
\end{equation}
\begin{equation}
|\Gamma({\sigma}+it)|\ll e^{-{\sigma}}\left|s^{s-\frac{1}{2}}\right|=e^{-{\sigma}} |s|^{{\sigma}-\frac{1}{2}}e^{-t\arg s},
\end{equation}since
 \begin{equation*}
\left|s^{s-\frac{1}{2}}\right|= e^{\operatorname{Re}\left(\left(s-\frac{1}{2}\right)\log s\right)}=e^{\left({\sigma}-\frac{1}{2}\right)\log |s|-t \arg s},
\end{equation*}
\begin{equation*}
\left|s^{s-\frac{1}{2}}\right|= e^{\operatorname{Re}\left(\left(s-\frac{1}{2}\right)\log s\right)}=e^{\left({\sigma}-\frac{1}{2}\right)\log |s|-t \arg s},
\end{equation*} where the principal branch of the logarithm in ![]() $\mathbb{C}\setminus \left(\left. \infty,0\right. \right]$ is chosen. Now observe that
$\mathbb{C}\setminus \left(\left. \infty,0\right. \right]$ is chosen. Now observe that ![]() $-t\arg s \leq 0$ when
$-t\arg s \leq 0$ when ![]() $-\pi \lt \arg s \lt \pi$, so (2.4) yields the bound
$-\pi \lt \arg s \lt \pi$, so (2.4) yields the bound
 \begin{equation}
|\Gamma({\sigma}+it)|\ll e^{-{\sigma}} |s|^{{\sigma}-\frac{1}{2}}.
\end{equation}
\begin{equation}
|\Gamma({\sigma}+it)|\ll e^{-{\sigma}} |s|^{{\sigma}-\frac{1}{2}}.
\end{equation} Whenever s satisfies ![]() $|t| \gt {\sigma} \gt 0$, we have
$|t| \gt {\sigma} \gt 0$, we have ![]() $|\arg s| \gt \frac{\pi}{4}$ and in this case, (2.4) gives the better bound
$|\arg s| \gt \frac{\pi}{4}$ and in this case, (2.4) gives the better bound
 \begin{equation}
|\Gamma({\sigma}+it)|\ll e^{-{\sigma}} |s|^{{\sigma}-\frac{1}{2}}e^{-|t|\frac{\pi}{4}}.
\end{equation}
\begin{equation}
|\Gamma({\sigma}+it)|\ll e^{-{\sigma}} |s|^{{\sigma}-\frac{1}{2}}e^{-|t|\frac{\pi}{4}}.
\end{equation} Taking ![]() $\beta_i=b_i+ic_i$, where
$\beta_i=b_i+ic_i$, where ![]() $b_i,c_i \in \mathbb{R}$, we can use the bound (2.6) for
$b_i,c_i \in \mathbb{R}$, we can use the bound (2.6) for ![]() $\Gamma(\alpha_is+\beta_i)$ whenever
$\Gamma(\alpha_is+\beta_i)$ whenever ![]() $|\operatorname{Im}(\alpha_is+\beta_i)| \gt \operatorname{Re}(\alpha_is+\beta_i)$, that is when
$|\operatorname{Im}(\alpha_is+\beta_i)| \gt \operatorname{Re}(\alpha_is+\beta_i)$, that is when  $t \gt {\sigma}+\frac{b_i-c_i}{\alpha_i}$ or
$t \gt {\sigma}+\frac{b_i-c_i}{\alpha_i}$ or  $t \lt -{\sigma}-\frac{b_i+c_i}{\alpha_i}$. Now, let us consider
$t \lt -{\sigma}-\frac{b_i+c_i}{\alpha_i}$. Now, let us consider  $T_1=\max_{i=1}^{r}{\left[N+\frac{b_i-c_i}{\alpha_i}\right]},\, T_2=\min_{i=1}^{r}{\left[-N-\frac{b_i+c_i}{\alpha_i}\right]} $. For N sufficiently large, we have
$T_1=\max_{i=1}^{r}{\left[N+\frac{b_i-c_i}{\alpha_i}\right]},\, T_2=\min_{i=1}^{r}{\left[-N-\frac{b_i+c_i}{\alpha_i}\right]} $. For N sufficiently large, we have ![]() $T_1 \gt 0$ and
$T_1 \gt 0$ and ![]() $T_2 \lt 0$. We write
$T_2 \lt 0$. We write
 \begin{align}
I_{22}&=\int_{N-iT}^{N+iT}\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds \notag \\
& =\left[\int_{-T}^{T_2}+\int_{T_2}^{T_1}+\int_{T_1}^{T}\right]\prod_{i=1}^{r} \Gamma(\alpha_i(N+it)+ \beta_i) x^{-(N+it)}idt.
\end{align}
\begin{align}
I_{22}&=\int_{N-iT}^{N+iT}\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds \notag \\
& =\left[\int_{-T}^{T_2}+\int_{T_2}^{T_1}+\int_{T_1}^{T}\right]\prod_{i=1}^{r} \Gamma(\alpha_i(N+it)+ \beta_i) x^{-(N+it)}idt.
\end{align}We will use (2.6) to estimate the first and third integral on the right-hand side above. We get
 \begin{align}
& \int_{T_1}^{T}\prod_{i=1}^{r}\left|\Gamma(\alpha_i(N+it)+ \beta_i)\right| x^{-N}dt\notag\\
& \quad \ll x^{-N}e^{-\sum_{i=1}^{r}(\alpha_i N+b_i)}\int_{T_1}^{T} e^{-\frac{\pi}{4}\sum_{i=1}^{r}|\alpha_i t+c_i|}\prod_{i=1}^{r}\notag\\
& \qquad \times \left|(\alpha_i N+b_i)+i(\alpha_i t+c_i)\right|^{\alpha_i N+b_i-\frac{1}{2}} dt.
\end{align}
\begin{align}
& \int_{T_1}^{T}\prod_{i=1}^{r}\left|\Gamma(\alpha_i(N+it)+ \beta_i)\right| x^{-N}dt\notag\\
& \quad \ll x^{-N}e^{-\sum_{i=1}^{r}(\alpha_i N+b_i)}\int_{T_1}^{T} e^{-\frac{\pi}{4}\sum_{i=1}^{r}|\alpha_i t+c_i|}\prod_{i=1}^{r}\notag\\
& \qquad \times \left|(\alpha_i N+b_i)+i(\alpha_i t+c_i)\right|^{\alpha_i N+b_i-\frac{1}{2}} dt.
\end{align} Letting ![]() $\gamma=\max_{i=1}^{r}{\left\{|\alpha_i|,|b_i|,|c_i|\right\}}$, we have
$\gamma=\max_{i=1}^{r}{\left\{|\alpha_i|,|b_i|,|c_i|\right\}}$, we have ![]() $\left|\alpha_i N+b_i+i(\alpha_i t+c_i)\right| \leq \gamma(N+t+2)$, keeping in mind that t > 0. Using the notation
$\left|\alpha_i N+b_i+i(\alpha_i t+c_i)\right| \leq \gamma(N+t+2)$, keeping in mind that t > 0. Using the notation  $d_F^{'}=\sum_{i=1}^{r}\alpha_i$, (2.8) is
$d_F^{'}=\sum_{i=1}^{r}\alpha_i$, (2.8) is
 \begin{equation*}
\ll_{b_i,c_i,r} x^{-N} e^{-Nd_F^{'}} \gamma^{Nd_F^{'}} \int_{T_1}^{T} e^{-\frac{\pi}{4}td_F^{'}} (N+t+2)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}}dt.
\end{equation*}
\begin{equation*}
\ll_{b_i,c_i,r} x^{-N} e^{-Nd_F^{'}} \gamma^{Nd_F^{'}} \int_{T_1}^{T} e^{-\frac{\pi}{4}td_F^{'}} (N+t+2)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}}dt.
\end{equation*} We now make the change of variable ![]() $u=N+t+2$ to see that the above expression is
$u=N+t+2$ to see that the above expression is
 \begin{align}
&\ll_{b_i,c_i,r,d_F^{'}} x^{-N} e^{-Nd_F^{'}} \gamma^{Nd_F^{'}} \int_{N+T_1+2}^{N+T+2} e^{-\frac{\pi}{4}ud_F^{'}}e^{\frac{\pi}{4}Nd_F^{'}} u^{\left(Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}\right)} du \nonumber\\
&\ll_{\alpha_i,b_i,c_i,r} x^{-N} e^{-Nd_F^{'}\left(1-\frac{\pi}{4}\right)} \gamma^{Nd_F^{'}} \int_{N+T_1+2}^{N+T+2} e^{-\frac{\pi}{4}ud_F^{'}} u^{\left(Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}\right)} du.
\end{align}
\begin{align}
&\ll_{b_i,c_i,r,d_F^{'}} x^{-N} e^{-Nd_F^{'}} \gamma^{Nd_F^{'}} \int_{N+T_1+2}^{N+T+2} e^{-\frac{\pi}{4}ud_F^{'}}e^{\frac{\pi}{4}Nd_F^{'}} u^{\left(Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}\right)} du \nonumber\\
&\ll_{\alpha_i,b_i,c_i,r} x^{-N} e^{-Nd_F^{'}\left(1-\frac{\pi}{4}\right)} \gamma^{Nd_F^{'}} \int_{N+T_1+2}^{N+T+2} e^{-\frac{\pi}{4}ud_F^{'}} u^{\left(Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}\right)} du.
\end{align} Putting  $v=\frac{\pi}{4}ud_F^{'}$, the integrand above is
$v=\frac{\pi}{4}ud_F^{'}$, the integrand above is
 \begin{equation*}e^{-v}\left(\frac{v}{\frac{\pi}{4}d_F^{'}}\right)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}} \ll e^{-v} v^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}}, \end{equation*}
\begin{equation*}e^{-v}\left(\frac{v}{\frac{\pi}{4}d_F^{'}}\right)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}} \ll e^{-v} v^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}}, \end{equation*}so that (2.9) is
 \begin{align*}
&\ll_{\alpha_i,b_i,c_i,r} x^{-N} e^{-Nd_F^{'}\left(1-\frac{\pi}{4}\right)} \gamma^{Nd_F^{'}} \Gamma\left(Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}+1\right)\nonumber\\
&\ll_{\alpha_i,b_i,c_i,r} x^{-N} e^{-Nd_F^{'}\left(1-\frac{\pi}{4}\right)} \gamma^{Nd_F^{'}} \left(Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}+1\right)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}+\frac{1}{2}}e^{-Nd_F^{'}},\nonumber
\end{align*}
\begin{align*}
&\ll_{\alpha_i,b_i,c_i,r} x^{-N} e^{-Nd_F^{'}\left(1-\frac{\pi}{4}\right)} \gamma^{Nd_F^{'}} \Gamma\left(Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}+1\right)\nonumber\\
&\ll_{\alpha_i,b_i,c_i,r} x^{-N} e^{-Nd_F^{'}\left(1-\frac{\pi}{4}\right)} \gamma^{Nd_F^{'}} \left(Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}+1\right)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}+\frac{1}{2}}e^{-Nd_F^{'}},\nonumber
\end{align*} using the estimate (2.5). For N sufficiently large, we can write  $Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}+1\leq CNd_F^{'}$, for some C > 0. We also have
$Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}+1\leq CNd_F^{'}$, for some C > 0. We also have  $\sum_{i=1}^{r}b_i-\frac{r}{2}+\frac{1}{2}\leq C_1$ for some constant C 1 depending on
$\sum_{i=1}^{r}b_i-\frac{r}{2}+\frac{1}{2}\leq C_1$ for some constant C 1 depending on ![]() $\boldsymbol \alpha, \boldsymbol \beta$. Thus, the above expression is
$\boldsymbol \alpha, \boldsymbol \beta$. Thus, the above expression is
 \begin{align}
&\ll_{\boldsymbol \alpha,\boldsymbol \beta} x^{-N} e^{-Nd_F^{'}\left(2-\frac{\pi}{4}\right)} \gamma^{Nd_F^{'}}\left(CNd_F^{'}\right)^{Nd_F^{'}} \left(CNd_F^{'}\right)^{C_1}\nonumber\\
&\ll_{\boldsymbol \alpha,\boldsymbol \beta} x^{-N} e^{-Nd_F^{'}\left(2-\frac{\pi}{4}\right)} (C\gamma)^{Nd_F^{'}}\left(Nd_F^{'}\right)^{Nd_F^{'}+C_1}
\end{align}
\begin{align}
&\ll_{\boldsymbol \alpha,\boldsymbol \beta} x^{-N} e^{-Nd_F^{'}\left(2-\frac{\pi}{4}\right)} \gamma^{Nd_F^{'}}\left(CNd_F^{'}\right)^{Nd_F^{'}} \left(CNd_F^{'}\right)^{C_1}\nonumber\\
&\ll_{\boldsymbol \alpha,\boldsymbol \beta} x^{-N} e^{-Nd_F^{'}\left(2-\frac{\pi}{4}\right)} (C\gamma)^{Nd_F^{'}}\left(Nd_F^{'}\right)^{Nd_F^{'}+C_1}
\end{align} \begin{align}
& \ll \exp \left(-Nd_F^{'}\left[\frac{\log x}{d_F^{'}}+2-\frac{\pi}{4}-\log C\gamma \right.\right.\notag\\
& \quad \left.\left. -\left(1+\frac{C_1}{Nd_F^{'}}\right)\log Nd_F^{'}+O_{\boldsymbol \alpha, \boldsymbol \beta}\left(\frac{1}{Nd_F^{'}}\right)\right]\right).
\end{align}
\begin{align}
& \ll \exp \left(-Nd_F^{'}\left[\frac{\log x}{d_F^{'}}+2-\frac{\pi}{4}-\log C\gamma \right.\right.\notag\\
& \quad \left.\left. -\left(1+\frac{C_1}{Nd_F^{'}}\right)\log Nd_F^{'}+O_{\boldsymbol \alpha, \boldsymbol \beta}\left(\frac{1}{Nd_F^{'}}\right)\right]\right).
\end{align} It can be checked that in order to ensure that the expression in square brackets is positive as ![]() $x\rightarrow \infty$, it is enough to choose
$x\rightarrow \infty$, it is enough to choose
 \begin{equation*}
N=\frac{A}{d_F^{'}}x^{\frac{1}{d_F^{'}}}, \nonumber
\end{equation*}
\begin{equation*}
N=\frac{A}{d_F^{'}}x^{\frac{1}{d_F^{'}}}, \nonumber
\end{equation*} for some A > 0 satisfying ![]() $\log A \lt 2-\frac{\pi}{4}-\log C\gamma$. This means that (2.11) is
$\log A \lt 2-\frac{\pi}{4}-\log C\gamma$. This means that (2.11) is
 \begin{equation}
\ll \exp(-C_2x^{\frac{1}{d_F^{'}}}),
\end{equation}
\begin{equation}
\ll \exp(-C_2x^{\frac{1}{d_F^{'}}}),
\end{equation} for some positive constant C 2, depending upon ![]() $\boldsymbol \alpha, \boldsymbol \beta$. In a similar way, we also get
$\boldsymbol \alpha, \boldsymbol \beta$. In a similar way, we also get
 \begin{equation}
\int_{-T}^{T_2}\prod_{i=1}^{r} \Gamma(\alpha_i(N+it)+ \beta_i) x^{-(N+it)}idt \ll \exp(-C_3x^{\frac{1}{d_F^{'}}}),
\end{equation}
\begin{equation}
\int_{-T}^{T_2}\prod_{i=1}^{r} \Gamma(\alpha_i(N+it)+ \beta_i) x^{-(N+it)}idt \ll \exp(-C_3x^{\frac{1}{d_F^{'}}}),
\end{equation} for some positive constant ![]() $C_3 = C_3(\boldsymbol \alpha, \boldsymbol \beta)$.
$C_3 = C_3(\boldsymbol \alpha, \boldsymbol \beta)$.
We now turn to the middle integral in (2.7). Using the bound (2.5), we get
 \begin{align*}
\int_{T_2}^{T_1}\prod_{i=1}^{r}\left|\Gamma(\alpha_i(N+it)+ \beta_i)\right| x^{-N}dt
\end{align*}
\begin{align*}
\int_{T_2}^{T_1}\prod_{i=1}^{r}\left|\Gamma(\alpha_i(N+it)+ \beta_i)\right| x^{-N}dt
\end{align*} \begin{align}
\ll x^{-N}e^{-\sum_{i=1}^{r}(\alpha_i N+b_i)}\int_{T_2}^{T_1} \prod_{i=1}^{r}\left|(\alpha_i N+b_i)+i(\alpha_i t+c_i)\right|^{\alpha_i N+b_i-\frac{1}{2}} dt.
\end{align}
\begin{align}
\ll x^{-N}e^{-\sum_{i=1}^{r}(\alpha_i N+b_i)}\int_{T_2}^{T_1} \prod_{i=1}^{r}\left|(\alpha_i N+b_i)+i(\alpha_i t+c_i)\right|^{\alpha_i N+b_i-\frac{1}{2}} dt.
\end{align} Taking γ as defined previously, we have ![]() $\left|\alpha_i N+b_i+i(\alpha_i t+c_i)\right| \leq \gamma(N+|t|+2)$. With the notation
$\left|\alpha_i N+b_i+i(\alpha_i t+c_i)\right| \leq \gamma(N+|t|+2)$. With the notation ![]() $d_F^{'}$ as before, (2.14) is
$d_F^{'}$ as before, (2.14) is
 \begin{equation*}
\ll_{b_i,r} x^{-N} e^{-Nd_F^{'}} \gamma^{Nd_F^{'}} \int_{T_2}^{T_1}(N+|t|+2)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}} dt.
\end{equation*}
\begin{equation*}
\ll_{b_i,r} x^{-N} e^{-Nd_F^{'}} \gamma^{Nd_F^{'}} \int_{T_2}^{T_1}(N+|t|+2)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}} dt.
\end{equation*} As ![]() $T_1,T_2$ are both
$T_1,T_2$ are both ![]() $\ll N$, we have
$\ll N$, we have ![]() $|t| \ll N$ in the domain of the above integral. Hence, for some C > 0, the above expression is
$|t| \ll N$ in the domain of the above integral. Hence, for some C > 0, the above expression is
 \begin{align*}
&\ll_{b_i,r} x^{-N} e^{-Nd_F^{'}} \gamma^{Nd_F^{'}} (CN)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}}\int_{T_2}^{T_1} dt\\
&\ll_{b_i,r} x^{-N} e^{-Nd_F^{'}} (C\gamma)^{Nd_F^{'}} N^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}+1}.
\end{align*}
\begin{align*}
&\ll_{b_i,r} x^{-N} e^{-Nd_F^{'}} \gamma^{Nd_F^{'}} (CN)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}}\int_{T_2}^{T_1} dt\\
&\ll_{b_i,r} x^{-N} e^{-Nd_F^{'}} (C\gamma)^{Nd_F^{'}} N^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}+1}.
\end{align*} Similar to as done for (2.10), the choice  $N=Bx^{\frac{1}{d_F^{'}}}$, for some B > 0 satisfying
$N=Bx^{\frac{1}{d_F^{'}}}$, for some B > 0 satisfying ![]() $\log B \lt 1-\log C\gamma$, yields
$\log B \lt 1-\log C\gamma$, yields
 \begin{equation}
\int_{T_2}^{T_1}\prod_{i=1}^{r}\Gamma(\alpha_i(N+it)+ \beta_i) x^{-N}dt \ll \exp(-C_4x^{\frac{1}{d_F^{'}}}),
\end{equation}
\begin{equation}
\int_{T_2}^{T_1}\prod_{i=1}^{r}\Gamma(\alpha_i(N+it)+ \beta_i) x^{-N}dt \ll \exp(-C_4x^{\frac{1}{d_F^{'}}}),
\end{equation} for some positive constant ![]() $C_4= C_4(\boldsymbol \alpha, \boldsymbol \beta)$. Finally, we choose
$C_4= C_4(\boldsymbol \alpha, \boldsymbol \beta)$. Finally, we choose  $N=Dx^{\frac{1}{d_F^{'}}}$, where
$N=Dx^{\frac{1}{d_F^{'}}}$, where ![]() $D= \min \{A, B\}$ and combine (2.7), (2.12), (2.13), and (2.15), to get
$D= \min \{A, B\}$ and combine (2.7), (2.12), (2.13), and (2.15), to get
 \begin{equation*}
I_{22}\ll \exp(-Cx^{\frac{1}{d_F^{'}}}),
\end{equation*}
\begin{equation*}
I_{22}\ll \exp(-Cx^{\frac{1}{d_F^{'}}}),
\end{equation*} for some ![]() $C=C(\boldsymbol \alpha, \boldsymbol \beta) \gt 0$. Turning to I 23, we have
$C=C(\boldsymbol \alpha, \boldsymbol \beta) \gt 0$. Turning to I 23, we have
 \begin{align*}
I_{23} & =\int_{N+ iT}^{a + iT}\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds \notag\\
& \ll \int_{a}^{N}\prod_{i=1}^{r}\left|\Gamma(\alpha_i({\sigma}+iT)+ \beta_i)\right| x^{-{\sigma}}d{\sigma}\\
& \ll e^{-\frac{\pi}{4}T}\!\int_{a}^{N}\!\!\! e^{-\sum_{i=1}^{r}(\alpha_i {\sigma}+b_i)}\!\prod_{i=1}^{r}\left|(\alpha_i {\sigma}+b_i)+i(\alpha_i T+c_i)\right|^{\alpha_i {\sigma}+b_i-\frac{1}{2}}x^{-{\sigma}} d{\sigma},
\end{align*}
\begin{align*}
I_{23} & =\int_{N+ iT}^{a + iT}\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds \notag\\
& \ll \int_{a}^{N}\prod_{i=1}^{r}\left|\Gamma(\alpha_i({\sigma}+iT)+ \beta_i)\right| x^{-{\sigma}}d{\sigma}\\
& \ll e^{-\frac{\pi}{4}T}\!\int_{a}^{N}\!\!\! e^{-\sum_{i=1}^{r}(\alpha_i {\sigma}+b_i)}\!\prod_{i=1}^{r}\left|(\alpha_i {\sigma}+b_i)+i(\alpha_i T+c_i)\right|^{\alpha_i {\sigma}+b_i-\frac{1}{2}}x^{-{\sigma}} d{\sigma},
\end{align*} upon using the bound (2.6). Using the same notations  $\gamma, d_F^{'}$ as before, the above is
$\gamma, d_F^{'}$ as before, the above is
 \begin{equation}
\ll_{b_i,r} e^{-\frac{\pi}{4}T} e^{-ad_F^{'}}\gamma^{Nd_F^{'}}(N+T+2)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}}x^{-a}N,
\end{equation}
\begin{equation}
\ll_{b_i,r} e^{-\frac{\pi}{4}T} e^{-ad_F^{'}}\gamma^{Nd_F^{'}}(N+T+2)^{Nd_F^{'}+\sum_{i=1}^{r}b_i-\frac{r}{2}}x^{-a}N,
\end{equation} considering the upper bound of the integrand in the interval ![]() $a \leq {\sigma} \leq N$ for
$a \leq {\sigma} \leq N$ for ![]() $x \gt 1,T \gt 0$ and sufficiently large N. If we take
$x \gt 1,T \gt 0$ and sufficiently large N. If we take ![]() $T\gg N^2$, due to the dominance of the exponential term in (2.16), the contribution from this horizontal integral is negligible. In a similar manner, we can also bound I 21.
$T\gg N^2$, due to the dominance of the exponential term in (2.16), the contribution from this horizontal integral is negligible. In a similar manner, we can also bound I 21.
We now consider the integrals I 1 and I 3. We write
 \begin{align*}
I_3 & =\int_{a+iT}^{a+i\infty}\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds \\
&\ll \int_{T}^{\infty}\prod_{i=1}^{r}\left|\Gamma(\alpha_i(a+it)+ \beta_i)\right| x^{-a}dt \\
&\ll \int_{T}^{\infty}e^{-\frac{\pi}{2}\sum_{i=1}^{r}|\alpha_it+c_i|}\prod_{i=1}^{r} |\alpha_it+c_i|^{\alpha_ia+b_i-\frac{1}{2}}x^{-a}dt,
\end{align*}
\begin{align*}
I_3 & =\int_{a+iT}^{a+i\infty}\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) x^{-s}ds \\
&\ll \int_{T}^{\infty}\prod_{i=1}^{r}\left|\Gamma(\alpha_i(a+it)+ \beta_i)\right| x^{-a}dt \\
&\ll \int_{T}^{\infty}e^{-\frac{\pi}{2}\sum_{i=1}^{r}|\alpha_it+c_i|}\prod_{i=1}^{r} |\alpha_it+c_i|^{\alpha_ia+b_i-\frac{1}{2}}x^{-a}dt,
\end{align*}using the Stirling formula (2.3). For sufficiently large T, the above integral becomes negligible due to exponential decay, as seen for (2.16). The same applies to I 1. Thus, we conclude that
 \begin{equation*}
Z_{\boldsymbol \alpha,\boldsymbol \beta}(x)\ll \exp{\left(-cx^{\frac{1}{d_F^{'}}}\right)},
\end{equation*}
\begin{equation*}
Z_{\boldsymbol \alpha,\boldsymbol \beta}(x)\ll \exp{\left(-cx^{\frac{1}{d_F^{'}}}\right)},
\end{equation*} where c is a positive constant that depends upon ![]() $\boldsymbol \alpha, \boldsymbol \beta$.
$\boldsymbol \alpha, \boldsymbol \beta$.
As a corollary to the above lemma, we have the following estimate for the integral ![]() $Y_{\boldsymbol \alpha,\boldsymbol\beta}(x)$, which was defined in (1.15).
$Y_{\boldsymbol \alpha,\boldsymbol\beta}(x)$, which was defined in (1.15).
Corollary 2.10. We have as ![]() $x\rightarrow \infty$,
$x\rightarrow \infty$,
 \begin{equation*}
Y_{\boldsymbol \alpha,\boldsymbol\beta}(x) \ll \exp{\left(-cx^{\frac{1}{1+d_F^{'}}}\right)},
\end{equation*}
\begin{equation*}
Y_{\boldsymbol \alpha,\boldsymbol\beta}(x) \ll \exp{\left(-cx^{\frac{1}{1+d_F^{'}}}\right)},
\end{equation*} where  $d_F^{'}=\sum_{i=1}^{r}\alpha_i$ and c is some positive constant depending on α and β.
$d_F^{'}=\sum_{i=1}^{r}\alpha_i$ and c is some positive constant depending on α and β.
In the following lemma, we prove an asymptotic formula for an integral involving multiple gamma factors. Our result is different from those existing in the literature, such as lemma 1 of Chandrasekharan and Narasimhan [Reference Chandrasekharan and Narasimhan20], since the functional equation considered by us entails conjugates of βi appearing in the gamma factors in the numerator. Moreover, our result is not restricted to integer values of ρ and holds for any large real value of ρ.
Lemma 2.11. Let  ${\delta} \geq 0, d_F^{'}=\sum_{i=1}^{r}\alpha_i, a \gt 0$ be sufficiently large and
${\delta} \geq 0, d_F^{'}=\sum_{i=1}^{r}\alpha_i, a \gt 0$ be sufficiently large and  ${\rho} \gt (2a-{\delta})d_F^{'}-1$. Consider
${\rho} \gt (2a-{\delta})d_F^{'}-1$. Consider
 \begin{equation*}
I_{\rho}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta}_i)}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}x^{{\rho}+{\delta}-s}ds.
\end{equation*}
\begin{equation*}
I_{\rho}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta}_i)}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}x^{{\rho}+{\delta}-s}ds.
\end{equation*} Then for any positive integer m, we have as ![]() $x\rightarrow \infty$,
$x\rightarrow \infty$,
 \begin{align*}I_\rho(x)&=\sum_{n=0}^mA_nx^\frac{\omega^\prime-n-2i\nu-\frac12}{2d_F^{{}^\prime}}\cos{\left((h^{-1}x)^\frac1{2d_F^{{}^\prime}}+\pi{(d_F^{\prime}\gamma+\frac n2+i\nu-\mu)}\right)}\nonumber \\ & \qquad\qquad+O\left(x^\frac{\omega^\prime-m-\frac32}{2d_F^{{}^\prime}}\right),\end{align*}
\begin{align*}I_\rho(x)&=\sum_{n=0}^mA_nx^\frac{\omega^\prime-n-2i\nu-\frac12}{2d_F^{{}^\prime}}\cos{\left((h^{-1}x)^\frac1{2d_F^{{}^\prime}}+\pi{(d_F^{\prime}\gamma+\frac n2+i\nu-\mu)}\right)}\nonumber \\ & \qquad\qquad+O\left(x^\frac{\omega^\prime-m-\frac32}{2d_F^{{}^\prime}}\right),\end{align*} where An are some constants, and writing ![]() $\beta_i=b_i+ic_i$, we have
$\beta_i=b_i+ic_i$, we have
 \begin{align}
\nu & =\sum_{i=1}^{r}c_i, \, \omega'=d_F^{'}{\delta}+(2d_F^{'}-1){\rho},\, \notag\\
h & =\exp \left\{\sum_{i=1}^{r}2\alpha_i\log\alpha_i-2d_F^{'} \log2d_F^{'}\right\},\, \notag\\
\mu & =\frac{1}{2}+\sum_{i=1}^{r}\left(\beta_i-\frac{1}{2}\right), \nonumber\\
\gamma & = -\left(\frac{{\delta}}{2}+\frac{{\rho}}{2d_F^{'}}+\frac{1}{4d_F^{'}}\right),\ \notag\\
k & =\sqrt{2\pi}(2d_F^{'})^{-2d_F^{'}\gamma+2i\nu+\frac{1}{2}} \exp{\left(-\sum_{i=1}^{r}(\alpha_i{\delta}+2ic_i)\log \alpha_i\right)}.
\end{align}
\begin{align}
\nu & =\sum_{i=1}^{r}c_i, \, \omega'=d_F^{'}{\delta}+(2d_F^{'}-1){\rho},\, \notag\\
h & =\exp \left\{\sum_{i=1}^{r}2\alpha_i\log\alpha_i-2d_F^{'} \log2d_F^{'}\right\},\, \notag\\
\mu & =\frac{1}{2}+\sum_{i=1}^{r}\left(\beta_i-\frac{1}{2}\right), \nonumber\\
\gamma & = -\left(\frac{{\delta}}{2}+\frac{{\rho}}{2d_F^{'}}+\frac{1}{4d_F^{'}}\right),\ \notag\\
k & =\sqrt{2\pi}(2d_F^{'})^{-2d_F^{'}\gamma+2i\nu+\frac{1}{2}} \exp{\left(-\sum_{i=1}^{r}(\alpha_i{\delta}+2ic_i)\log \alpha_i\right)}.
\end{align}Proof. Let us define
 \begin{equation}
G_{\rho}(s):=\frac{\Gamma(\delta-s) \prod_{j=1}^{r}\Gamma(\alpha_js+\bar{\beta}_j)}{\Gamma(1+\delta-s+\rho)\prod_{j=1}^{r}\Gamma(\alpha_j(\delta-s)+\beta_j)}.
\end{equation}
\begin{equation}
G_{\rho}(s):=\frac{\Gamma(\delta-s) \prod_{j=1}^{r}\Gamma(\alpha_js+\bar{\beta}_j)}{\Gamma(1+\delta-s+\rho)\prod_{j=1}^{r}\Gamma(\alpha_j(\delta-s)+\beta_j)}.
\end{equation}Taking logarithm on both the sides above, we write
 \begin{align*}
\log{G_{\rho}(s)} & =\log{\Gamma(\delta-s)}+\sum_{j=1}^{r}\log{\Gamma(\alpha_js+\bar{\beta}_j)}-\log{\Gamma(1+\delta-s+\rho)}\notag\\
& \quad -\sum_{j=1}^{r}\log{\Gamma(\alpha_j(\delta-s)+\beta_j)}.
\end{align*}
\begin{align*}
\log{G_{\rho}(s)} & =\log{\Gamma(\delta-s)}+\sum_{j=1}^{r}\log{\Gamma(\alpha_js+\bar{\beta}_j)}-\log{\Gamma(1+\delta-s+\rho)}\notag\\
& \quad -\sum_{j=1}^{r}\log{\Gamma(\alpha_j(\delta-s)+\beta_j)}.
\end{align*} For the remainder of the proof, ![]() $C_n \, (n=1,\dots, m)$ will denote constants whose values may differ from line to line. Using lemma 2.7, we obtain
$C_n \, (n=1,\dots, m)$ will denote constants whose values may differ from line to line. Using lemma 2.7, we obtain
 \begin{align}
\log{G_{\rho}(s)}&=\left({\delta}-s-\frac{1}{2}\right)\log{(-s)}+s+\sum_{j=1}^{r}\left\{\left(\alpha_js+\bar{\beta}_j-\frac{1}{2}\right)\log{\alpha_js} -\alpha_js \right\} \nonumber\\
& \quad -\left(1+\delta-s+\rho-\frac{1}{2}\right)\log{(-s)}-s \notag\\
& \quad -\sum_{j=1}^{r}\left\{\left(\alpha_j({\delta}-s)+\beta_j-\frac{1}{2}\right)\log{(-\alpha_js)}+\alpha_js \right\} \nonumber\\
& \quad +\sum_{n=1}^{m}C_{n}s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right) \nonumber\\
& =\left(d_F^{'}s+2d_F^{'}\gamma-\mu\right)\log{(-s)}+\left(d_F^{'}s+\sum_{j=1}^{r}\bar{\beta}_j-\frac{r}{2}\right)\log s\notag\\
& \quad -2d_F^{'}s+2s\sum_{j=1}^{r}\alpha_j\log \alpha_j \nonumber\\
& \quad -\sum_{j=1}^{r}\alpha_j {\delta} \log \alpha_j-2i \sum_{j=1}^{r}c_j \log \alpha_j +
\sum_{n=1}^{m}C_{n} s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right),
\end{align}
\begin{align}
\log{G_{\rho}(s)}&=\left({\delta}-s-\frac{1}{2}\right)\log{(-s)}+s+\sum_{j=1}^{r}\left\{\left(\alpha_js+\bar{\beta}_j-\frac{1}{2}\right)\log{\alpha_js} -\alpha_js \right\} \nonumber\\
& \quad -\left(1+\delta-s+\rho-\frac{1}{2}\right)\log{(-s)}-s \notag\\
& \quad -\sum_{j=1}^{r}\left\{\left(\alpha_j({\delta}-s)+\beta_j-\frac{1}{2}\right)\log{(-\alpha_js)}+\alpha_js \right\} \nonumber\\
& \quad +\sum_{n=1}^{m}C_{n}s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right) \nonumber\\
& =\left(d_F^{'}s+2d_F^{'}\gamma-\mu\right)\log{(-s)}+\left(d_F^{'}s+\sum_{j=1}^{r}\bar{\beta}_j-\frac{r}{2}\right)\log s\notag\\
& \quad -2d_F^{'}s+2s\sum_{j=1}^{r}\alpha_j\log \alpha_j \nonumber\\
& \quad -\sum_{j=1}^{r}\alpha_j {\delta} \log \alpha_j-2i \sum_{j=1}^{r}c_j \log \alpha_j +
\sum_{n=1}^{m}C_{n} s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right),
\end{align} where ![]() $\gamma, \mu$ are as defined in (2.17). For
$\gamma, \mu$ are as defined in (2.17). For ![]() $v_0=1$ and some constants
$v_0=1$ and some constants ![]() $v_n, n=1, \dots, m$, to be chosen later, we define
$v_n, n=1, \dots, m$, to be chosen later, we define
 \begin{align}
F_n^{{\rho}}(s)&:=\frac{v_nkh^s \Gamma\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-n\right)}{\Gamma\left(\frac{1}{2}-d_F^{'}s-2d_F^{'}\gamma+\mu \right)\Gamma\left(\frac{1}{2}+d_F^{'}s+2d_F^{'}\gamma-\mu \right)}
\end{align}
\begin{align}
F_n^{{\rho}}(s)&:=\frac{v_nkh^s \Gamma\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-n\right)}{\Gamma\left(\frac{1}{2}-d_F^{'}s-2d_F^{'}\gamma+\mu \right)\Gamma\left(\frac{1}{2}+d_F^{'}s+2d_F^{'}\gamma-\mu \right)}
\end{align} \begin{align}
&=\frac{v_nk}{\pi}h^s \Gamma\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-n\right)\cos\left(\pi(d_F^{'}s+2d_F^{'}\gamma-\mu)\right),
\end{align}
\begin{align}
&=\frac{v_nk}{\pi}h^s \Gamma\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-n\right)\cos\left(\pi(d_F^{'}s+2d_F^{'}\gamma-\mu)\right),
\end{align} with ![]() $\gamma, \nu, \mu, h, k$ as defined in (2.17). Taking logarithm of
$\gamma, \nu, \mu, h, k$ as defined in (2.17). Taking logarithm of ![]() $F_0^{{\rho}}(s)$, we have
$F_0^{{\rho}}(s)$, we have
 \begin{align*}
\log F_0^{{\rho}}(s) & =\log k +s\log h+\log \Gamma\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu\right)\notag\\
& \quad -\log \Gamma\left(\frac{1}{2}-d_F^{'}s-2d_F^{'}\gamma+\mu \right) \\ & \quad -\log \Gamma\left(\frac{1}{2}+d_F^{'}s+2d_F^{'}\gamma-\mu \right).
\end{align*}
\begin{align*}
\log F_0^{{\rho}}(s) & =\log k +s\log h+\log \Gamma\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu\right)\notag\\
& \quad -\log \Gamma\left(\frac{1}{2}-d_F^{'}s-2d_F^{'}\gamma+\mu \right) \\ & \quad -\log \Gamma\left(\frac{1}{2}+d_F^{'}s+2d_F^{'}\gamma-\mu \right).
\end{align*} Using the values of ![]() $k,h$ and lemma 2.7, we get
$k,h$ and lemma 2.7, we get
 \begin{align}
\log F_0^{{\rho}}(s)&=\! \left(\! -2d_F^{'}\gamma+2i\nu+\frac{1}{2}\right) \log 2d_F^{'}+\frac{\log{2\pi}}{2}\notag\\
& \quad -\sum_{j=1}^{r}\alpha_j {\delta} \log \alpha_j-2i\sum_{j=1}^{r}c_j \log \alpha_j \nonumber\\
& \quad +2s\sum_{j=1}^{r}\alpha_j\log\alpha_j-2d_F^{'}s \log2d_F^{'}\notag\\
& \quad +\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-\frac{1}{2}\right)\log 2d_F^{'}s-2d_F^{'}s \nonumber\\
& \quad +\frac{\log{2\pi}}{2}-\log{(-d_F^{'}s)}\left(-d_F^{'}s-2d_F^{'}\gamma+\mu \right)\notag\\
& \quad -d_F^{'}s-\frac{\log{2\pi}}{2}
-\left(d_F^{'}s+2d_F^{'}\gamma-\mu \right)\log d_F^{'}s \nonumber\\
& \quad +d_F^{'}s-\frac{\log{2\pi}}{2}+\sum_{n=1}^{m}C_ns^{-n}+\left(\frac{1}{|s|^{m+1}}\right) \nonumber\\
&=\left(d_F^{'}s+2d_F^{'}\gamma-\mu\right)\log{(-s)}\notag\\
& \quad +\left(d_F^{'}s+\sum_{j=1}^{r}\bar{\beta}_j-\frac{r}{2}\right)\log s-2d_F^{'}s+2s\sum_{j=1}^{r}\alpha_j\log \alpha_j \nonumber\\
& \quad -\sum_{j=1}^{r}\alpha_j {\delta} \log \alpha_j-2i \sum_{j=1}^{r}c_j \log \alpha_j +
\sum_{n=1}^{m}C_{n} s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right),
\end{align}
\begin{align}
\log F_0^{{\rho}}(s)&=\! \left(\! -2d_F^{'}\gamma+2i\nu+\frac{1}{2}\right) \log 2d_F^{'}+\frac{\log{2\pi}}{2}\notag\\
& \quad -\sum_{j=1}^{r}\alpha_j {\delta} \log \alpha_j-2i\sum_{j=1}^{r}c_j \log \alpha_j \nonumber\\
& \quad +2s\sum_{j=1}^{r}\alpha_j\log\alpha_j-2d_F^{'}s \log2d_F^{'}\notag\\
& \quad +\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-\frac{1}{2}\right)\log 2d_F^{'}s-2d_F^{'}s \nonumber\\
& \quad +\frac{\log{2\pi}}{2}-\log{(-d_F^{'}s)}\left(-d_F^{'}s-2d_F^{'}\gamma+\mu \right)\notag\\
& \quad -d_F^{'}s-\frac{\log{2\pi}}{2}
-\left(d_F^{'}s+2d_F^{'}\gamma-\mu \right)\log d_F^{'}s \nonumber\\
& \quad +d_F^{'}s-\frac{\log{2\pi}}{2}+\sum_{n=1}^{m}C_ns^{-n}+\left(\frac{1}{|s|^{m+1}}\right) \nonumber\\
&=\left(d_F^{'}s+2d_F^{'}\gamma-\mu\right)\log{(-s)}\notag\\
& \quad +\left(d_F^{'}s+\sum_{j=1}^{r}\bar{\beta}_j-\frac{r}{2}\right)\log s-2d_F^{'}s+2s\sum_{j=1}^{r}\alpha_j\log \alpha_j \nonumber\\
& \quad -\sum_{j=1}^{r}\alpha_j {\delta} \log \alpha_j-2i \sum_{j=1}^{r}c_j \log \alpha_j +
\sum_{n=1}^{m}C_{n} s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right),
\end{align}upon simplification. From (2.19) and (2.22), we obtain
 \begin{equation*}
\log{G_{\rho}(s)}= \log F_0^{{\rho}}(s)+\sum_{n=1}^{m}C_{n} s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right).
\end{equation*}
\begin{equation*}
\log{G_{\rho}(s)}= \log F_0^{{\rho}}(s)+\sum_{n=1}^{m}C_{n} s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right).
\end{equation*}Thus, we have
 \begin{align*}
G_{\rho}(s)&=F_0^{{\rho}}(s)\left[1+\sum_{n=1}^{m}C_{n} s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right)\right]\\
&=F_0^{{\rho}}(s)\left[1+\sum_{n=1}^{m}\frac{C_{n}}{\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-1\right)\cdots\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-n\right)}\right.\notag\\
& \quad \left. +O\left(\frac{1}{|s|^{m+1}}\right)\right]\\
&=F_0^{{\rho}}(s)+\sum_{n=1}^{m}\frac{C_{n}kh^s \Gamma\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu\right)\cos\left(\pi(d_F^{'}s+2d_F^{'}\gamma-\mu)\right)}
{\pi \left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-1\right)\cdots\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-n\right)} \notag\\
& \quad +O\left(\frac{|F_0^{{\rho}}(s)|}{|s|^{m+1}}\right),
\end{align*}
\begin{align*}
G_{\rho}(s)&=F_0^{{\rho}}(s)\left[1+\sum_{n=1}^{m}C_{n} s^{-n}+O\left(\frac{1}{|s|^{m+1}}\right)\right]\\
&=F_0^{{\rho}}(s)\left[1+\sum_{n=1}^{m}\frac{C_{n}}{\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-1\right)\cdots\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-n\right)}\right.\notag\\
& \quad \left. +O\left(\frac{1}{|s|^{m+1}}\right)\right]\\
&=F_0^{{\rho}}(s)+\sum_{n=1}^{m}\frac{C_{n}kh^s \Gamma\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu\right)\cos\left(\pi(d_F^{'}s+2d_F^{'}\gamma-\mu)\right)}
{\pi \left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-1\right)\cdots\left(2d_F^{'}s+2d_F^{'}\gamma-2i\nu-n\right)} \notag\\
& \quad +O\left(\frac{|F_0^{{\rho}}(s)|}{|s|^{m+1}}\right),
\end{align*} upon substituting the value of ![]() $F_0^{{\rho}}(s)$ from (2.21). Since
$F_0^{{\rho}}(s)$ from (2.21). Since ![]() $z\Gamma(z)=\Gamma(z+1)$, putting
$z\Gamma(z)=\Gamma(z+1)$, putting ![]() $v_n=C_n$ and using (2.21), we obtain
$v_n=C_n$ and using (2.21), we obtain
 \begin{align}
G_{\rho}(s)=\sum_{n=0}^{m}F^{{\rho}}_n(s)+O\left(\frac{|F^{{\rho}}_0(s)|}{|s|^{m+1}}\right).
\end{align}
\begin{align}
G_{\rho}(s)=\sum_{n=0}^{m}F^{{\rho}}_n(s)+O\left(\frac{|F^{{\rho}}_0(s)|}{|s|^{m+1}}\right).
\end{align} We will integrate ![]() $G_\rho(s)$ along a contour Cρ defined as follows. Let
$G_\rho(s)$ along a contour Cρ defined as follows. Let  $c_{\rho}=\frac{d_F^{'} {\delta}+{\rho}}{2d_F^{'}}-\epsilon, 0 \lt \epsilon \lt \frac{1}{4d_F^{'}}$. The contour Cρ consists of the line
$c_{\rho}=\frac{d_F^{'} {\delta}+{\rho}}{2d_F^{'}}-\epsilon, 0 \lt \epsilon \lt \frac{1}{4d_F^{'}}$. The contour Cρ consists of the line ![]() $(c_{\rho}-i\infty, c_{\rho}-iT)$, followed by the three sides
$(c_{\rho}-i\infty, c_{\rho}-iT)$, followed by the three sides ![]() $[c_{\rho}-iT, c_{\rho}+u-iT], [c_{\rho}+u-iT, c_{\rho}+u+iT], [c_{\rho}+u+iT, c_{\rho}+iT]$ of a rectangle, followed by the line
$[c_{\rho}-iT, c_{\rho}+u-iT], [c_{\rho}+u-iT, c_{\rho}+u+iT], [c_{\rho}+u+iT, c_{\rho}+iT]$ of a rectangle, followed by the line ![]() $(c_{\rho}+iT, c_{\rho}+i\infty)$. Here, we choose u and T sufficiently large, so that all the singularities of
$(c_{\rho}+iT, c_{\rho}+i\infty)$. Here, we choose u and T sufficiently large, so that all the singularities of ![]() $F^{{\rho}}_n(s)$ for
$F^{{\rho}}_n(s)$ for ![]() $n=0, \ldots, m$, lie to the left of Cρ. If we take a contour C which is the same as Cρ, with cρ replaced by some
$n=0, \ldots, m$, lie to the left of Cρ. If we take a contour C which is the same as Cρ, with cρ replaced by some  $c \lt -\frac{1}{2}$, and
$c \lt -\frac{1}{2}$, and ![]() $u,T$ chosen so that all the singularities of
$u,T$ chosen so that all the singularities of  $\Gamma(s)\cos\left(\frac{\pi}{2}s+\alpha \right)x^{-s}$ lie to the left of C, then by lemma 2.6,
$\Gamma(s)\cos\left(\frac{\pi}{2}s+\alpha \right)x^{-s}$ lie to the left of C, then by lemma 2.6,
 \begin{equation}
\frac{1}{2\pi i}\int_{C}\Gamma(s)\cos\left(\frac{\pi}{2}s+\alpha \right)x^{-s}ds=\cos(x+\alpha),
\end{equation}
\begin{equation}
\frac{1}{2\pi i}\int_{C}\Gamma(s)\cos\left(\frac{\pi}{2}s+\alpha \right)x^{-s}ds=\cos(x+\alpha),
\end{equation} because of the contribution of residues at the poles ![]() $s=-n,0\leq n \lt |c|$, of the integrand. Multiplying (2.23) by
$s=-n,0\leq n \lt |c|$, of the integrand. Multiplying (2.23) by  $\frac{x^{{\rho}+{\delta}-s}}{2\pi i}$ and integrating with respect to s along the curve Cρ, we have
$\frac{x^{{\rho}+{\delta}-s}}{2\pi i}$ and integrating with respect to s along the curve Cρ, we have
 \begin{equation}
\frac{x^{{\rho}+{\delta}}}{2\pi i}\int_{C_{\rho}}G_{\rho}(s) x^{-s}ds=\frac{x^{{\rho}+{\delta}}}{2\pi i} \left[\sum_{n=0}^{m}\int_{C_{\rho}}F^{{\rho}}_n(s)x^{-s}ds+\int_{C_{\rho}}O\left(\frac{|F^{{\rho}}_0(s)|}{|s|^{m+1}}\right)x^{-s}ds\right].
\end{equation}
\begin{equation}
\frac{x^{{\rho}+{\delta}}}{2\pi i}\int_{C_{\rho}}G_{\rho}(s) x^{-s}ds=\frac{x^{{\rho}+{\delta}}}{2\pi i} \left[\sum_{n=0}^{m}\int_{C_{\rho}}F^{{\rho}}_n(s)x^{-s}ds+\int_{C_{\rho}}O\left(\frac{|F^{{\rho}}_0(s)|}{|s|^{m+1}}\right)x^{-s}ds\right].
\end{equation}We will evaluate both the integrals on the right-hand side above. Using (2.21), we have
 \begin{align*}
&\int_{C_\rho}F^{\rho}_n(s)x^{-s}ds
\\
&=
\frac{v_n k}{\pi}
\int_{C_\rho}\Gamma \left(2d_F^{'}s+2d_F^{'}\gamma -2i \nu-n\right)
\cos\left(\pi(d_F^{'}s+2d_F^{'}\gamma-\mu)\right)
\left(h^{-1}x\right)^{-s}ds
\\
&(
h^{-1}x)^{\gamma-\frac{n+2i\nu}{2d_F^{'}}} \frac{v_nk}{2\pi d_F^{'}} \int_{C_\rho^{'}} \Gamma(z)
\cos\left(\frac{\pi}{2}z+\pi\left(d_F^{'}\gamma+\frac{n}{2}+ i\nu- \mu\right)\right)
(h^{-1}x)^{\frac{-z}{2d_F^{'}}}dz,
\end{align*}
\begin{align*}
&\int_{C_\rho}F^{\rho}_n(s)x^{-s}ds
\\
&=
\frac{v_n k}{\pi}
\int_{C_\rho}\Gamma \left(2d_F^{'}s+2d_F^{'}\gamma -2i \nu-n\right)
\cos\left(\pi(d_F^{'}s+2d_F^{'}\gamma-\mu)\right)
\left(h^{-1}x\right)^{-s}ds
\\
&(
h^{-1}x)^{\gamma-\frac{n+2i\nu}{2d_F^{'}}} \frac{v_nk}{2\pi d_F^{'}} \int_{C_\rho^{'}} \Gamma(z)
\cos\left(\frac{\pi}{2}z+\pi\left(d_F^{'}\gamma+\frac{n}{2}+ i\nu- \mu\right)\right)
(h^{-1}x)^{\frac{-z}{2d_F^{'}}}dz,
\end{align*} upon changing the variable  $2d_F^{'}s+2d_F^{'}\gamma-2i\nu-n$ to z. The change of variable shifts the curve Cρ to
$2d_F^{'}s+2d_F^{'}\gamma-2i\nu-n$ to z. The change of variable shifts the curve Cρ to ![]() $C_{\rho}^{'}$, with cρ replaced by
$C_{\rho}^{'}$, with cρ replaced by  $c{'}_{\rho} \lt -\frac{1}{2}$. Using (2.24), we obtain
$c{'}_{\rho} \lt -\frac{1}{2}$. Using (2.24), we obtain
 \begin{equation}\frac1{2\pi i}\int_{C_\rho}F_n^\rho(s)x^{-s}ds=A_nx^{\gamma-\frac{n+2i\nu}{2d_F^{'}}}\cos\left((h^{-1}x)^\frac1{2d_F^{'}}+\pi\left(d_F^{'}\gamma+\frac n2+i\nu-\mu\right)\right),\end{equation}
\begin{equation}\frac1{2\pi i}\int_{C_\rho}F_n^\rho(s)x^{-s}ds=A_nx^{\gamma-\frac{n+2i\nu}{2d_F^{'}}}\cos\left((h^{-1}x)^\frac1{2d_F^{'}}+\pi\left(d_F^{'}\gamma+\frac n2+i\nu-\mu\right)\right),\end{equation} where  $A_n=\frac{v_nk}{2\pi d_F^{'}}h^{\frac{n+2i\nu}{2d_F^{'}}-\gamma}$. In order to deal with the second integral in (2.25), we write
$A_n=\frac{v_nk}{2\pi d_F^{'}}h^{\frac{n+2i\nu}{2d_F^{'}}-\gamma}$. In order to deal with the second integral in (2.25), we write
 \begin{equation}
\frac{1}{2\pi i}\int_{C_{\rho}}O\left(\frac{|F^{{\rho}}_0(s)|}{|s|^{m+1}}\right)x^{-s}ds=\frac{1}{2\pi i}\int_{C_{\rho}+\frac{m+1}{2d_F^{'}}}O\left(\frac{|F^{{\rho}}_0(s)|}{|s|^{m+1}}\right)x^{-s}ds,
\end{equation}
\begin{equation}
\frac{1}{2\pi i}\int_{C_{\rho}}O\left(\frac{|F^{{\rho}}_0(s)|}{|s|^{m+1}}\right)x^{-s}ds=\frac{1}{2\pi i}\int_{C_{\rho}+\frac{m+1}{2d_F^{'}}}O\left(\frac{|F^{{\rho}}_0(s)|}{|s|^{m+1}}\right)x^{-s}ds,
\end{equation} where  $C_{\rho}+\frac{m+1}{2d_F^{'}}$ denotes the contour obtained by shifting Cρ to the right by
$C_{\rho}+\frac{m+1}{2d_F^{'}}$ denotes the contour obtained by shifting Cρ to the right by  $\frac{m+1}{2d_F^{'}}$. This shift is justified as follows. Since all the singularities of the integrand lie to the left of Cρ, it is analytic between the contours Cρ and
$\frac{m+1}{2d_F^{'}}$. This shift is justified as follows. Since all the singularities of the integrand lie to the left of Cρ, it is analytic between the contours Cρ and  $C_{\rho}+\frac{m+1}{2d_F^{'}}$. Using (2.20), the Stirling formula (2.3) and the fact that
$C_{\rho}+\frac{m+1}{2d_F^{'}}$. Using (2.20), the Stirling formula (2.3) and the fact that ![]() $\cos(s)\ll \exp(|\operatorname{Im}(s)|)$, writing
$\cos(s)\ll \exp(|\operatorname{Im}(s)|)$, writing ![]() $s={\sigma}+it$, in the region
$s={\sigma}+it$, in the region  $c_{\rho} \leq {\sigma} \leq c_{\rho}+\frac{m+1}{2d_F^{'}}$, we see as
$c_{\rho} \leq {\sigma} \leq c_{\rho}+\frac{m+1}{2d_F^{'}}$, we see as ![]() $|t| \to \infty$,
$|t| \to \infty$,
 \begin{equation}
\frac{|F^{{\rho}}_0(s)| }{|s|^{m+1}}\ll
\frac{1}{|s|^{m+1}} |2d_F^{'}t-2\nu|^{2d_F^{'}\left(c_{\rho}+\tfrac{m+1}{2d_F^{'}}\right)+2d_F^{'}\gamma-\frac{1}{2}}
\ll |t|^{-1-2\epsilon d_F^{'}},
\end{equation}
\begin{equation}
\frac{|F^{{\rho}}_0(s)| }{|s|^{m+1}}\ll
\frac{1}{|s|^{m+1}} |2d_F^{'}t-2\nu|^{2d_F^{'}\left(c_{\rho}+\tfrac{m+1}{2d_F^{'}}\right)+2d_F^{'}\gamma-\frac{1}{2}}
\ll |t|^{-1-2\epsilon d_F^{'}},
\end{equation} upon putting  $c_{\rho}=\frac{d_F^{'} {\delta}+{\rho}}{2d_F^{'}}-\epsilon, \gamma=-\left(\frac{{\delta}}{2}+\frac{{\rho}}{2d_F^{'}}+\frac{1}{4d_F^{'}}\right)$ and using
$c_{\rho}=\frac{d_F^{'} {\delta}+{\rho}}{2d_F^{'}}-\epsilon, \gamma=-\left(\frac{{\delta}}{2}+\frac{{\rho}}{2d_F^{'}}+\frac{1}{4d_F^{'}}\right)$ and using ![]() $|s|\sim |t|$. Hence, by analyticity and decay of the integrand which makes the contribution of the horizontal integrals zero as
$|s|\sim |t|$. Hence, by analyticity and decay of the integrand which makes the contribution of the horizontal integrals zero as ![]() $|t|\to \infty$, (2.27) is justified.
$|t|\to \infty$, (2.27) is justified.
For any large fixed ϵ > 0, the right-hand side of (2.27) is
 \begin{equation}
\ll x^{-c_{\rho}-\frac{m+1}{2d_F^{'}}}
\left( \int_{|t| \gt \epsilon }\frac{|F^{{\rho}}_0(s)|}{|s|^{m+1}}dt + O_\epsilon(1) \right)
\ll x^{-c_{\rho}-\frac{m+1}{2d_F^{'}}},
\end{equation}
\begin{equation}
\ll x^{-c_{\rho}-\frac{m+1}{2d_F^{'}}}
\left( \int_{|t| \gt \epsilon }\frac{|F^{{\rho}}_0(s)|}{|s|^{m+1}}dt + O_\epsilon(1) \right)
\ll x^{-c_{\rho}-\frac{m+1}{2d_F^{'}}},
\end{equation} using (2.28). Combining (2.25), (2.26), and (2.29), recalling that  $c_{\rho}=\frac{d_F^{'} {\delta}+{\rho}}{2d_F^{'}}-\epsilon$, and putting
$c_{\rho}=\frac{d_F^{'} {\delta}+{\rho}}{2d_F^{'}}-\epsilon$, and putting  $\omega'=d_F^{'}{\delta}+(2d_F^{'}-1){\rho}$, we have
$\omega'=d_F^{'}{\delta}+(2d_F^{'}-1){\rho}$, we have
 \begin{align*}&\frac{x^{\rho+\delta}}{2\pi i}\int_{C_\rho}G_\rho(s)x^{-s}ds=\sum_{n=0}^mA_nx^\frac{\omega'-n-2i\nu-\frac12}{2d_F^{'}}\\&\qquad\qquad\cos\left((h^{-1}x)^\frac1{2d_F^{'}}+\pi\left(d_F^{'}\gamma+\frac n2+i\nu-\mu\right)\right)+O\left(x^{\frac{\omega'-m-1}{2d_F^{'}}+\epsilon}\right)\\\\&\qquad\qquad=\sum_{n=0}^{m-1}A_nx^\frac{\omega'-n-2i\nu-\frac12}{2d_F^{'}}\cos\left((h^{-1}x)^\frac1{2d_F^{'}}+\pi\left(d_F^{'}\gamma+\frac n2+i\nu-\mu\right)\right)\\&\qquad\qquad\quad+O\left(x^\frac{\omega'-m-\frac12}{2d_F^{'}}+x^{\frac{\omega'-m-1}{2d_F^{'}}+\epsilon}\right).\end{align*}
\begin{align*}&\frac{x^{\rho+\delta}}{2\pi i}\int_{C_\rho}G_\rho(s)x^{-s}ds=\sum_{n=0}^mA_nx^\frac{\omega'-n-2i\nu-\frac12}{2d_F^{'}}\\&\qquad\qquad\cos\left((h^{-1}x)^\frac1{2d_F^{'}}+\pi\left(d_F^{'}\gamma+\frac n2+i\nu-\mu\right)\right)+O\left(x^{\frac{\omega'-m-1}{2d_F^{'}}+\epsilon}\right)\\\\&\qquad\qquad=\sum_{n=0}^{m-1}A_nx^\frac{\omega'-n-2i\nu-\frac12}{2d_F^{'}}\cos\left((h^{-1}x)^\frac1{2d_F^{'}}+\pi\left(d_F^{'}\gamma+\frac n2+i\nu-\mu\right)\right)\\&\qquad\qquad\quad+O\left(x^\frac{\omega'-m-\frac12}{2d_F^{'}}+x^{\frac{\omega'-m-1}{2d_F^{'}}+\epsilon}\right).\end{align*} Since  $\frac{\omega'-m-1}{2d_F^{'}}+\epsilon \lt \frac{\omega'-m-\frac{1}{2}}{2d_F^{'}}$ for
$\frac{\omega'-m-1}{2d_F^{'}}+\epsilon \lt \frac{\omega'-m-\frac{1}{2}}{2d_F^{'}}$ for  $0 \lt \epsilon \lt \frac{1}{4d_F^{'}}$, we obtain
$0 \lt \epsilon \lt \frac{1}{4d_F^{'}}$, we obtain
 \begin{align}
&\frac{x^{\rho+\delta}}{2\pi i}\int_{C_\rho}G_\rho(s) x^{-s}ds\nonumber\\
&=\sum_{n=0}^{m-1} A_n x^{\frac{\omega'-n-2i\nu-\frac{1}{2}}{2d_F^{'}}}
\cos\left((h^{-1}x)^{\frac{1}{2d_F^{'}}}+\pi\left(d_F^{'}\gamma+\frac{n}{2}+ i\nu- \mu\right)\right)\nonumber \\
&+ O\left( x^{\frac{\omega'-m-\frac{1}{2}}{2d_F^{'}}}\right).
\end{align}
\begin{align}
&\frac{x^{\rho+\delta}}{2\pi i}\int_{C_\rho}G_\rho(s) x^{-s}ds\nonumber\\
&=\sum_{n=0}^{m-1} A_n x^{\frac{\omega'-n-2i\nu-\frac{1}{2}}{2d_F^{'}}}
\cos\left((h^{-1}x)^{\frac{1}{2d_F^{'}}}+\pi\left(d_F^{'}\gamma+\frac{n}{2}+ i\nu- \mu\right)\right)\nonumber \\
&+ O\left( x^{\frac{\omega'-m-\frac{1}{2}}{2d_F^{'}}}\right).
\end{align}To complete the proof, we need to show that
 \begin{equation}
\int_{C_{\rho}}G_{\rho}(s) x^{-s}ds=\int_{a-i\infty}^{a+i \infty}G_{\rho}(s) x^{-s}ds,
\end{equation}
\begin{equation}
\int_{C_{\rho}}G_{\rho}(s) x^{-s}ds=\int_{a-i\infty}^{a+i \infty}G_{\rho}(s) x^{-s}ds,
\end{equation} for a sufficiently large. Note that (2.30) holds for the contour Cρ, with any ![]() $u,T$ sufficiently large. Denoting
$u,T$ sufficiently large. Denoting ![]() $c_{\rho}+u$ as a, by definition of the contour Cρ, we have
$c_{\rho}+u$ as a, by definition of the contour Cρ, we have
 \begin{align}
\int_{C_{\rho}}G_{\rho}(s) x^{-s}ds&=\left[\int_{c_{\rho}-i\infty}^{c_{\rho}-iT}+\int_{c_{\rho}-iT}^{a-iT}+\int_{a-iT}^{a+iT}+\int_{a+iT}^{c_{\rho}+iT}+\int_{c_{\rho}+iT}^{c_{\rho}+i\infty}\right]G_{\rho}(s) x^{-s}ds.
\end{align}
\begin{align}
\int_{C_{\rho}}G_{\rho}(s) x^{-s}ds&=\left[\int_{c_{\rho}-i\infty}^{c_{\rho}-iT}+\int_{c_{\rho}-iT}^{a-iT}+\int_{a-iT}^{a+iT}+\int_{a+iT}^{c_{\rho}+iT}+\int_{c_{\rho}+iT}^{c_{\rho}+i\infty}\right]G_{\rho}(s) x^{-s}ds.
\end{align} We now claim that the horizontal integrals given by the second and fourth terms on the right-hand side above, vanish as ![]() $T\rightarrow \infty$. We use (2.18) and the Stirling formula (2.3) to obtain after some simplification,
$T\rightarrow \infty$. We use (2.18) and the Stirling formula (2.3) to obtain after some simplification,
 \begin{equation*}
G_{\rho}(s) \ll |T|^{-1-{\rho}+(2a-{\delta})d_F^{'}},
\end{equation*}
\begin{equation*}
G_{\rho}(s) \ll |T|^{-1-{\rho}+(2a-{\delta})d_F^{'}},
\end{equation*} which is o(1) as ![]() $T\rightarrow \infty$, whenever
$T\rightarrow \infty$, whenever  ${\rho} \gt (2a-{\delta})d_F^{'}-1$. This justifies the vanishing of the above-mentioned horizontal integrals in (2.32). As
${\rho} \gt (2a-{\delta})d_F^{'}-1$. This justifies the vanishing of the above-mentioned horizontal integrals in (2.32). As ![]() $T\to \infty$, the remaining integrals in (2.32) yield the right-hand side of (2.31), as needed.
$T\to \infty$, the remaining integrals in (2.32) yield the right-hand side of (2.31), as needed.
3. Proof of theorem 1.2
Let us start with the Mellin inversion of F(s). We choose ![]() $a \gt \max{\{0,{\sigma}_a,{\sigma}_b\}}$ and T large
enough such that the rectangle R with vertices
$a \gt \max{\{0,{\sigma}_a,{\sigma}_b\}}$ and T large
enough such that the rectangle R with vertices ![]() $a\pm iT, {\delta}-a \pm iT$ encloses all the singularities of F(s). From the definition of F(s) and from (1.18), we have
$a\pm iT, {\delta}-a \pm iT$ encloses all the singularities of F(s). From the definition of F(s) and from (1.18), we have
 \begin{align}
\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}F(s) x^{-s}ds
&=\lim_{T\rightarrow \infty} \frac{1}{2 \pi i}\int_{a-iT}^{a+iT}\prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)\phi(s)x^{-s}ds \nonumber\\
&=\frac{1}{2\pi i} \int_{a-i\infty}^{a+i\infty} \sum_{n=1}^{\infty}a_n \prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)(\lambda_nx)^{-s}ds.
\end{align}
\begin{align}
\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}F(s) x^{-s}ds
&=\lim_{T\rightarrow \infty} \frac{1}{2 \pi i}\int_{a-iT}^{a+iT}\prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)\phi(s)x^{-s}ds \nonumber\\
&=\frac{1}{2\pi i} \int_{a-i\infty}^{a+i\infty} \sum_{n=1}^{\infty}a_n \prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)(\lambda_nx)^{-s}ds.
\end{align}By lemma 2.9, we have
 \begin{align}
\sum_{n=1}^{\infty}a_n\frac{1}{2\pi i} \int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)(\lambda_nx)^{-s}ds
&\ll \sum_{n=1}^{\infty}|a_n| \exp{\Big(-c(\lambda_nx)^{\frac{1}{d_F^{'}}}\Big)} \nonumber\\
&\ll \sum_{n=1}^{\infty}|a_n| (\lambda_nx)^{-a},
\end{align}
\begin{align}
\sum_{n=1}^{\infty}a_n\frac{1}{2\pi i} \int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)(\lambda_nx)^{-s}ds
&\ll \sum_{n=1}^{\infty}|a_n| \exp{\Big(-c(\lambda_nx)^{\frac{1}{d_F^{'}}}\Big)} \nonumber\\
&\ll \sum_{n=1}^{\infty}|a_n| (\lambda_nx)^{-a},
\end{align} which is absolutely convergent since ![]() $a \gt {\sigma}_a$, where σa is the abscissa of absolute convergence of
$a \gt {\sigma}_a$, where σa is the abscissa of absolute convergence of ![]() $\phi(s)$. This justifies the interchange of summation and integration in (3.1), to yield
$\phi(s)$. This justifies the interchange of summation and integration in (3.1), to yield
 \begin{align}
\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}F(s) x^{-s}ds =\sum_{n=1}^{\infty}a_n\frac{1}{2\pi i} \int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)(\lambda_nx)^{-s}ds.
\end{align}
\begin{align}
\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}F(s) x^{-s}ds =\sum_{n=1}^{\infty}a_n\frac{1}{2\pi i} \int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)(\lambda_nx)^{-s}ds.
\end{align} We will now obtain a different expression for the left-hand side of (3.3) in order to derive the modular relation. Consider a curve C lying inside the rectangle R such that C encloses all the singularities of F(s). As all the singularities of ![]() $F(s)x^{-s}$ lie inside C, by Cauchy’s residue theorem, we get
$F(s)x^{-s}$ lie inside C, by Cauchy’s residue theorem, we get
 \begin{align}
& \frac{1}{2 \pi i}\int_{a-iT}^{a+iT}F(s) x^{-s}ds \notag\\
& \quad = \frac{1}{2 \pi i}\int_{C} F(s) x^{-s}ds-\frac{1}{2 \pi i}\left[\int_{a+iT}^{\delta-a+iT}+\int_{\delta-a+iT}^{\delta-a-iT}+\int_{\delta-a-iT}^{a-iT}\right]F(s) x^{-s}ds.
\end{align}
\begin{align}
& \frac{1}{2 \pi i}\int_{a-iT}^{a+iT}F(s) x^{-s}ds \notag\\
& \quad = \frac{1}{2 \pi i}\int_{C} F(s) x^{-s}ds-\frac{1}{2 \pi i}\left[\int_{a+iT}^{\delta-a+iT}+\int_{\delta-a+iT}^{\delta-a-iT}+\int_{\delta-a-iT}^{a-iT}\right]F(s) x^{-s}ds.
\end{align} We will show that the integrals on the horizontal lines will tend to zero as ![]() $T \rightarrow \infty$. Using lemma 2.4, we first show that
$T \rightarrow \infty$. Using lemma 2.4, we first show that
uniformly in the strip ![]() ${\delta}-a \leq \operatorname{Re}(s)\leq a$ as
${\delta}-a \leq \operatorname{Re}(s)\leq a$ as ![]() $|\operatorname{Im}(s)|\rightarrow \infty$. From definition 1.1, we see that
$|\operatorname{Im}(s)|\rightarrow \infty$. From definition 1.1, we see that ![]() $F(s)x^{-s}=\chi(s)(Qx)^{-s}$ satisfies the big O hypothesis required for lemma 2.4. Now it remains to verify the growth condition for
$F(s)x^{-s}=\chi(s)(Qx)^{-s}$ satisfies the big O hypothesis required for lemma 2.4. Now it remains to verify the growth condition for ![]() $F(s)x^{-s}$ on the two vertical lines,
$F(s)x^{-s}$ on the two vertical lines, ![]() $\operatorname{Re}(s)=a$ and
$\operatorname{Re}(s)=a$ and ![]() $\operatorname{Re}(s)={\delta}-a$.
$\operatorname{Re}(s)={\delta}-a$.
On the line ![]() $\operatorname{Re}(s)=a$, we have
$\operatorname{Re}(s)=a$, we have ![]() $\phi(s)x^{-s}=O(1)$ as
$\phi(s)x^{-s}=O(1)$ as ![]() $\phi(s)$ is absolutely convergent on this line. Writing
$\phi(s)$ is absolutely convergent on this line. Writing ![]() $s=a+it, \beta_i=b_i+ic_i$, and using the asymptotic formula (2.3), we have
$s=a+it, \beta_i=b_i+ic_i$, and using the asymptotic formula (2.3), we have
 \begin{equation*}
\left|\prod_{i=1}^{r}\Gamma(\alpha_i s+\beta_i)\right| \sim e^{-\frac{\pi}{2} \sum_{i=1}^{r} |\alpha_i t+c_i|} \prod_{i=1}^{r}|\alpha_i t+c_i|^{\alpha_i a+b_i-\frac{1}{2}}(\sqrt{2\pi})^r,
\end{equation*}
\begin{equation*}
\left|\prod_{i=1}^{r}\Gamma(\alpha_i s+\beta_i)\right| \sim e^{-\frac{\pi}{2} \sum_{i=1}^{r} |\alpha_i t+c_i|} \prod_{i=1}^{r}|\alpha_i t+c_i|^{\alpha_i a+b_i-\frac{1}{2}}(\sqrt{2\pi})^r,
\end{equation*} which implies that ![]() $\prod_{i=1}^{r}\Gamma(\alpha_i s+\beta_i)=o(1)$ as
$\prod_{i=1}^{r}\Gamma(\alpha_i s+\beta_i)=o(1)$ as ![]() $|t|\rightarrow \infty$. Thus,
$|t|\rightarrow \infty$. Thus, ![]() $F(s)x^{-s}=o(1)$ on the line
$F(s)x^{-s}=o(1)$ on the line ![]() $\operatorname{Re}(s)=a$.
$\operatorname{Re}(s)=a$.
Similarly, on the line ![]() $\operatorname{Re}(s)={\delta}-a$, we substitute the functional equation (1.9) and express
$\operatorname{Re}(s)={\delta}-a$, we substitute the functional equation (1.9) and express ![]() $F(s)x^{-s}$ by
$F(s)x^{-s}$ by
Again, using the absolute convergence of ![]() $\psi(s)$ on the line
$\psi(s)$ on the line ![]() $\operatorname{Re}(s)={\delta}-a$ and the Stirling formula for the Gamma factors, we conclude that
$\operatorname{Re}(s)={\delta}-a$ and the Stirling formula for the Gamma factors, we conclude that ![]() $F(s)x^{-s}=o(1)$ on
$F(s)x^{-s}=o(1)$ on ![]() $\operatorname{Re}(s)={\delta}-a$. Applying lemma 2.4, we have
$\operatorname{Re}(s)={\delta}-a$. Applying lemma 2.4, we have ![]() $F(s)x^{-s}=o(1)$, uniformly in the strip
$F(s)x^{-s}=o(1)$, uniformly in the strip ![]() ${\delta}-a\leq \operatorname{Re}(s)\leq a$ as
${\delta}-a\leq \operatorname{Re}(s)\leq a$ as ![]() $|t|\rightarrow \infty$ and hence both the horizontal integrals vanish as
$|t|\rightarrow \infty$ and hence both the horizontal integrals vanish as ![]() $|T|\rightarrow \infty$. Thus, from (3.4), we have
$|T|\rightarrow \infty$. Thus, from (3.4), we have
 \begin{align*}
\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}F(s) x^{-s}ds&=\frac{1}{2 \pi i}\int_{C} F(s) x^{-s}ds+\frac{1}{2 \pi i}\int_{\delta-a-i\infty}^{\delta-a+i\infty}F(s) x^{-s}ds \\
&=P(x)+\frac{1}{2 \pi i}\int_{\delta-a-i\infty}^{\delta-a+i\infty}w Q^{\delta-2s} \overline{G(\delta-\bar{s})}x^{-s}ds,
\end{align*}
\begin{align*}
\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}F(s) x^{-s}ds&=\frac{1}{2 \pi i}\int_{C} F(s) x^{-s}ds+\frac{1}{2 \pi i}\int_{\delta-a-i\infty}^{\delta-a+i\infty}F(s) x^{-s}ds \\
&=P(x)+\frac{1}{2 \pi i}\int_{\delta-a-i\infty}^{\delta-a+i\infty}w Q^{\delta-2s} \overline{G(\delta-\bar{s})}x^{-s}ds,
\end{align*} upon using the functional equation (1.9) and denoting the integral  $\frac{1}{2 \pi i}\int_{C} F(s) x^{-s}ds$ by P(x).
Now, we change the variable
$\frac{1}{2 \pi i}\int_{C} F(s) x^{-s}ds$ by P(x).
Now, we change the variable ![]() $\delta-s$ to s, to get
$\delta-s$ to s, to get
 \begin{align}
& \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}F(s) x^{-s}ds\notag\\
& \quad =P(x)+\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}w Q^{2s-\delta} \overline{G(\bar{s})}x^{-\delta+s}ds \nonumber\\
& \quad =P(x)+ \frac{\omega}{(xQ)^\delta}\sum_{n=1}^{\infty}\bar{b}(n)\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta_i})\bigg(\frac{\mu_n}{Q^2 x}\bigg)^{-s}ds,
\end{align}
\begin{align}
& \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}F(s) x^{-s}ds\notag\\
& \quad =P(x)+\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}w Q^{2s-\delta} \overline{G(\bar{s})}x^{-\delta+s}ds \nonumber\\
& \quad =P(x)+ \frac{\omega}{(xQ)^\delta}\sum_{n=1}^{\infty}\bar{b}(n)\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta_i})\bigg(\frac{\mu_n}{Q^2 x}\bigg)^{-s}ds,
\end{align}after interchanging the summation and integration, and using the definition of G(s). Again, the interchange can be justified by absolute convergence of the above sum as explained in (3.2). Combining (3.3) and (3.5), we get the modular relation (1.10).
4. Proof of theorem 1.3
To obtain the functional equation (1.9) from the modular relation (1.10), we start with the expression for ![]() $Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)$. From (1.11), for
$Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)$. From (1.11), for ![]() $x,a \gt 0$, we have
$x,a \gt 0$, we have
 \begin{equation*}
Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) (\lambda_nx)^{-s}ds.
\end{equation*}
\begin{equation*}
Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i) (\lambda_nx)^{-s}ds.
\end{equation*} Taking the Mellin transform, for ![]() $\operatorname{Re}(s)={\sigma} \gt \max{\{0, {\sigma}_a, {\sigma}_b\}}$, we write
$\operatorname{Re}(s)={\sigma} \gt \max{\{0, {\sigma}_a, {\sigma}_b\}}$, we write
 \begin{align*}
\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i)&= \int_{0}^{\infty} Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)(\lambda_nx)^{s-1} d(\lambda_nx)\\
&=\lambda_n^{s}\int_{0}^{\infty} Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx.
\end{align*}
\begin{align*}
\prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i)&= \int_{0}^{\infty} Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)(\lambda_nx)^{s-1} d(\lambda_nx)\\
&=\lambda_n^{s}\int_{0}^{\infty} Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx.
\end{align*} We multiply both sides by ![]() $Q^s a_{n}$ and then sum over n to get left-hand side of the functional equation (1.9):
$Q^s a_{n}$ and then sum over n to get left-hand side of the functional equation (1.9):
 \begin{equation}
Q^s \phi(s) \prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i)=Q^s \sum_{n=1}^{\infty} a_n \int_{0}^{\infty} Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx.
\end{equation}
\begin{equation}
Q^s \phi(s) \prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i)=Q^s \sum_{n=1}^{\infty} a_n \int_{0}^{\infty} Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx.
\end{equation}In order to interchange summation and integration in the above expression on the right-hand side, let us first check the absolute convergence of the same. Using lemma 2.9, we can write
 \begin{align}
\sum_{n=1}^{\infty} a_n \int_{0}^{\infty} Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx&\ll \sum_{n=1}^{\infty} |a_n| \int_{0}^{\infty} \exp{\big(-c(\lambda_nx)^{\frac{1}{d_F^{'}}}\big)}x^{{\sigma}-1} dx \nonumber\\
&\ll \sum_{n=1}^{\infty} |a_n| \lambda_n^{-{\sigma}} \int_{0}^{\infty} \exp{\big(-cy^{\frac{1}{d_F^{'}}}\big)}y^{{\sigma}-1} dy,
\end{align}
\begin{align}
\sum_{n=1}^{\infty} a_n \int_{0}^{\infty} Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx&\ll \sum_{n=1}^{\infty} |a_n| \int_{0}^{\infty} \exp{\big(-c(\lambda_nx)^{\frac{1}{d_F^{'}}}\big)}x^{{\sigma}-1} dx \nonumber\\
&\ll \sum_{n=1}^{\infty} |a_n| \lambda_n^{-{\sigma}} \int_{0}^{\infty} \exp{\big(-cy^{\frac{1}{d_F^{'}}}\big)}y^{{\sigma}-1} dy,
\end{align} after changing the variable λnx to y. Here, the sum ![]() $\sum_{n=1}^{\infty}a_n \lambda_n^{-{\sigma}}$ converges absolutely as
$\sum_{n=1}^{\infty}a_n \lambda_n^{-{\sigma}}$ converges absolutely as ![]() ${\sigma} \gt {\sigma}_a$ and the integral above converges due to the exponential decay of the integrand. Hence, we may interchange the order of summation and integration in (4.1), to obtain
${\sigma} \gt {\sigma}_a$ and the integral above converges due to the exponential decay of the integrand. Hence, we may interchange the order of summation and integration in (4.1), to obtain
 \begin{equation*}
Q^s F(s)= Q^s\bigg( \int_{0}^{1} \sum_{n=1}^{\infty} a_n Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx+\int_{1}^{\infty} \sum_{n=1}^{\infty} a_n Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx\bigg).
\end{equation*}
\begin{equation*}
Q^s F(s)= Q^s\bigg( \int_{0}^{1} \sum_{n=1}^{\infty} a_n Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx+\int_{1}^{\infty} \sum_{n=1}^{\infty} a_n Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx\bigg).
\end{equation*}Now, we apply the modular relation (1.10) to the first integral to get
 \begin{align}
Q^s F(s) &= Q^s\bigg( \int_{0}^{1} P(x)x^{s-1} dx+\int_{0}^{1} \Psi(1/x)x^{s-1} dx+\int_{1}^{\infty} \Phi(x)x^{s-1} dx\bigg)\nonumber\\
&=Q^s\bigg( \int_{0}^{1} P(x)x^{s-1} dx+\int_{1}^{\infty} (\Psi(x)x^{-s-1} + \Phi(x)x^{s-1}) dx\bigg)\nonumber\\
&=I_1+J_1 \quad \text{(say)},
\end{align}
\begin{align}
Q^s F(s) &= Q^s\bigg( \int_{0}^{1} P(x)x^{s-1} dx+\int_{0}^{1} \Psi(1/x)x^{s-1} dx+\int_{1}^{\infty} \Phi(x)x^{s-1} dx\bigg)\nonumber\\
&=Q^s\bigg( \int_{0}^{1} P(x)x^{s-1} dx+\int_{1}^{\infty} (\Psi(x)x^{-s-1} + \Phi(x)x^{s-1}) dx\bigg)\nonumber\\
&=I_1+J_1 \quad \text{(say)},
\end{align}where
 \begin{equation*}
\Phi(x)=\sum_{n=1}^{\infty} a_n Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx) \ \ \text{and} \,\, \Psi(x)= \frac{\omega x^\delta}{Q^\delta} \sum_{n=1}^{\infty} \bar{b}_n Z_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\left(\frac{\mu_nx}{Q^2}\right).
\end{equation*}
\begin{equation*}
\Phi(x)=\sum_{n=1}^{\infty} a_n Z_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx) \ \ \text{and} \,\, \Psi(x)= \frac{\omega x^\delta}{Q^\delta} \sum_{n=1}^{\infty} \bar{b}_n Z_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\left(\frac{\mu_nx}{Q^2}\right).
\end{equation*} This gives us an expression for the left-hand side of the desired functional equation (1.9) in terms of integrals involving ![]() $Z_{\boldsymbol \alpha,\boldsymbol\beta}(x)$. We now attempt to do this for the right-hand side of (1.9) in a similar manner. From (1.11), for
$Z_{\boldsymbol \alpha,\boldsymbol\beta}(x)$. We now attempt to do this for the right-hand side of (1.9) in a similar manner. From (1.11), for ![]() $x,a \gt 0$, we have
$x,a \gt 0$, we have
 \begin{equation*}
Z_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_nx}{Q^2}\bigg)=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r} \Gamma(\alpha_i s+ \bar{\beta_i}) \bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds.
\end{equation*}
\begin{equation*}
Z_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_nx}{Q^2}\bigg)=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \prod_{i=1}^{r} \Gamma(\alpha_i s+ \bar{\beta_i}) \bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds.
\end{equation*} Again, taking the Mellin transform, multiplying both sides by ![]() $\omega Q^s\bar{b}_n$, and summing over n, we get for
$\omega Q^s\bar{b}_n$, and summing over n, we get for ![]() $\operatorname{Re}(s) \gt \max{\{0, {\sigma}_a, {\sigma}_b\}}$,
$\operatorname{Re}(s) \gt \max{\{0, {\sigma}_a, {\sigma}_b\}}$,
 \begin{align*}
\omega Q^s \overline{G(\bar{s})}
&= \omega Q^{-s} \sum_{n=1}^{\infty} \bar{b}_n \int_{0}^{\infty} Z_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_nx}{Q^2}\bigg)x^{s-1} dx \\
&= \omega Q^{-s} \left[\int_{0}^{1}+ \int_{1}^{\infty}\right]\sum_{n=1}^{\infty} \bar{b}_n Z_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_nx}{Q^2}\bigg)x^{s-1} dx.
\end{align*}
\begin{align*}
\omega Q^s \overline{G(\bar{s})}
&= \omega Q^{-s} \sum_{n=1}^{\infty} \bar{b}_n \int_{0}^{\infty} Z_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_nx}{Q^2}\bigg)x^{s-1} dx \\
&= \omega Q^{-s} \left[\int_{0}^{1}+ \int_{1}^{\infty}\right]\sum_{n=1}^{\infty} \bar{b}_n Z_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_nx}{Q^2}\bigg)x^{s-1} dx.
\end{align*}Here the interchange is justified by using lemma 2.9 as demonstrated before in (4.2). Proceeding in a similar manner, we use the modular relation (1.10) in the first integral above, to obtain
 \begin{align}
\omega Q^s \overline{G(\bar{s})}&= \omega Q^{-s}\bigg( \frac{Q^\delta}{\omega}\int_{0}^{1} \frac{1}{x^\delta}\Big(\Phi(1/x)-P(1/x)\Big) x^{s-1}+ \frac{Q^\delta}{\omega}\int_{1}^{\infty}\Psi(x)x^{-\delta+s-1} dx\bigg) \nonumber\\
&=Q^{\delta-s}\left(-\int_{1}^{\infty}P(x)x^{\delta-s-1}dx+\int_{1}^{\infty}(\Psi(x)x^{-\delta+s-1}+\Phi(x)x^{\delta-s-1})dx\right)
\end{align}
\begin{align}
\omega Q^s \overline{G(\bar{s})}&= \omega Q^{-s}\bigg( \frac{Q^\delta}{\omega}\int_{0}^{1} \frac{1}{x^\delta}\Big(\Phi(1/x)-P(1/x)\Big) x^{s-1}+ \frac{Q^\delta}{\omega}\int_{1}^{\infty}\Psi(x)x^{-\delta+s-1} dx\bigg) \nonumber\\
&=Q^{\delta-s}\left(-\int_{1}^{\infty}P(x)x^{\delta-s-1}dx+\int_{1}^{\infty}(\Psi(x)x^{-\delta+s-1}+\Phi(x)x^{\delta-s-1})dx\right)
\end{align} On replacing s by ![]() $\delta-s$ in (4.4), we notice that J 1 and J 2 in (4.3) and (4.5), respectively, become equal, and by definition 2.1, I 1 and I 2 are equal upon analytic continuation into the domain D. Hence the functional equation (1.9) follows.
$\delta-s$ in (4.4), we notice that J 1 and J 2 in (4.3) and (4.5), respectively, become equal, and by definition 2.1, I 1 and I 2 are equal upon analytic continuation into the domain D. Hence the functional equation (1.9) follows.
5. Proof of theorem 1.4
We know that ![]() $\phi(s)=\sum_{n=1}^{\infty}a_n \lambda_n^{-s}$ and
$\phi(s)=\sum_{n=1}^{\infty}a_n \lambda_n^{-s}$ and ![]() $\psi(s)=\sum_{n=1}^{\infty}b_n \mu_n^{-s}$ converge absolutely for
$\psi(s)=\sum_{n=1}^{\infty}b_n \mu_n^{-s}$ converge absolutely for ![]() $\operatorname{Re}(s) \gt {\sigma}_a$ and
$\operatorname{Re}(s) \gt {\sigma}_a$ and ![]() $\operatorname{Re}(s) \gt {\sigma}_b$, respectively. Now take
$\operatorname{Re}(s) \gt {\sigma}_b$, respectively. Now take  $a={\sigma}_b+\frac{1}{4d_F^{'}}+\frac{m}{2d_F^{'}}$, where m is a sufficiently large integer such that
$a={\sigma}_b+\frac{1}{4d_F^{'}}+\frac{m}{2d_F^{'}}$, where m is a sufficiently large integer such that ![]() $a \gt \max {\{0, {\sigma}_a, {\sigma}_b\}}$ and the set S (as in definition 1.1) lies inside the strip
$a \gt \max {\{0, {\sigma}_a, {\sigma}_b\}}$ and the set S (as in definition 1.1) lies inside the strip ![]() $\delta-a \lt \operatorname{Re}(s) \lt a$. Using lemma 2.8, for
$\delta-a \lt \operatorname{Re}(s) \lt a$. Using lemma 2.8, for ![]() $\rho\geq0$, we can write
$\rho\geq0$, we can write
 \begin{equation}
\frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{\lambda_n \leqslant x}{} a_{n}(x-\lambda_n)^\rho=\frac{1}{2\pi i} \int_{a-i \infty}^{a+i \infty} \frac{\phi(s)\Gamma(s) x^{s+\rho}}{\Gamma(s+\rho+1)}ds .
\end{equation}
\begin{equation}
\frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{\lambda_n \leqslant x}{} a_{n}(x-\lambda_n)^\rho=\frac{1}{2\pi i} \int_{a-i \infty}^{a+i \infty} \frac{\phi(s)\Gamma(s) x^{s+\rho}}{\Gamma(s+\rho+1)}ds .
\end{equation} Let us define  $f(s):=\frac{\phi(s)\Gamma(s) x^{s+\rho}}{\Gamma(s+\rho+1)}$. We choose T to be large enough such that S lies inside the rectangle R with vertices
$f(s):=\frac{\phi(s)\Gamma(s) x^{s+\rho}}{\Gamma(s+\rho+1)}$. We choose T to be large enough such that S lies inside the rectangle R with vertices ![]() $a \pm iT$,
$a \pm iT$, ![]() $\delta-a\pm iT$. Subsequently, take a curve C inside R, such that no singularities of f(s) lie in the region between the rectangle R and the curve C. Using the Cauchy residue theorem, we have
$\delta-a\pm iT$. Subsequently, take a curve C inside R, such that no singularities of f(s) lie in the region between the rectangle R and the curve C. Using the Cauchy residue theorem, we have
 \begin{equation}
\frac{1}{2 \pi i}\int_{a-iT}^{a+iT}f(s) ds = \frac{1}{2 \pi i}\int_{C} f(s) ds-\frac{1}{2 \pi i}\bigg[\int_{a+iT}^{\delta-a+iT}+\int_{\delta-a+iT}^{\delta-a-iT}+\int_{\delta-a-iT}^{a-iT}\bigg]f(s)ds.
\end{equation}
\begin{equation}
\frac{1}{2 \pi i}\int_{a-iT}^{a+iT}f(s) ds = \frac{1}{2 \pi i}\int_{C} f(s) ds-\frac{1}{2 \pi i}\bigg[\int_{a+iT}^{\delta-a+iT}+\int_{\delta-a+iT}^{\delta-a-iT}+\int_{\delta-a-iT}^{a-iT}\bigg]f(s)ds.
\end{equation} In order to show that the horizontal integrals are negligible as ![]() $T\rightarrow \infty$, it is enough to show that
$T\rightarrow \infty$, it is enough to show that ![]() $f(s)=o(1)$ uniformly in the strip
$f(s)=o(1)$ uniformly in the strip ![]() ${\delta}-a \leq \operatorname{Re}(s) \leq a$. We will show this by applying lemma 2.4 to the function f(s).
${\delta}-a \leq \operatorname{Re}(s) \leq a$. We will show this by applying lemma 2.4 to the function f(s).
On the line ![]() $\operatorname{Re}(s)=a,\phi(s)$ converges absolutely and so we have
$\operatorname{Re}(s)=a,\phi(s)$ converges absolutely and so we have ![]() $\phi(s)x^{{\rho}+a}\ll 1$. Using Stirling’s formula (2.3), we find that
$\phi(s)x^{{\rho}+a}\ll 1$. Using Stirling’s formula (2.3), we find that
 \begin{equation}
\frac{\Gamma(s)}{\Gamma(s+{\rho}+1)} \sim |t|^{-{\rho}-1},
\end{equation}
\begin{equation}
\frac{\Gamma(s)}{\Gamma(s+{\rho}+1)} \sim |t|^{-{\rho}-1},
\end{equation} which is o(1) since ρ > 0. Hence we have ![]() $f(s)=o(1)$ on the line
$f(s)=o(1)$ on the line ![]() $\operatorname{Re}(s)=a$.
$\operatorname{Re}(s)=a$.
On the other vertical line ![]() $\operatorname{Re}(s)={\delta}-a$, we use the functional equation (1.9) and get
$\operatorname{Re}(s)={\delta}-a$, we use the functional equation (1.9) and get
 \begin{equation*}
f(s)= \frac{\phi(s)\Gamma(s) x^{s+\rho}}{\Gamma(s+\rho+1)}=\frac{\Gamma(s)\prod_{i=1}^{r}\Gamma(\alpha_i({\delta}-s)+\bar{\beta}_i)}{\Gamma(s+{\rho}+1)\prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)}\omega Q^{{\delta}-2s}\overline{\psi({\delta}-\bar{s})}.
\end{equation*}
\begin{equation*}
f(s)= \frac{\phi(s)\Gamma(s) x^{s+\rho}}{\Gamma(s+\rho+1)}=\frac{\Gamma(s)\prod_{i=1}^{r}\Gamma(\alpha_i({\delta}-s)+\bar{\beta}_i)}{\Gamma(s+{\rho}+1)\prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)}\omega Q^{{\delta}-2s}\overline{\psi({\delta}-\bar{s})}.
\end{equation*} Again, ![]() $\omega Q^{{\delta}-2s}\overline{\psi({\delta}-\bar{s})}\ll 1$ on
$\omega Q^{{\delta}-2s}\overline{\psi({\delta}-\bar{s})}\ll 1$ on ![]() $\operatorname{Re}(s)={\delta}-a$ since
$\operatorname{Re}(s)={\delta}-a$ since ![]() $\psi(s)$ converges absolutely for
$\psi(s)$ converges absolutely for ![]() $\operatorname{Re}(s) \gt {\sigma}_b$. Writing
$\operatorname{Re}(s) \gt {\sigma}_b$. Writing ![]() $\beta_i=b_i+ic_i$ and
$\beta_i=b_i+ic_i$ and ![]() $s={\delta}-a+it$, we apply Stirling’s formula (2.3) to get after some computations,
$s={\delta}-a+it$, we apply Stirling’s formula (2.3) to get after some computations,
 \begin{equation*}
\frac{\Gamma(s)\prod_{i=1}^{r}\Gamma(\alpha_i({\delta}-s)+\bar{\beta}_i)}{\Gamma(s+{\rho}+1)\prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)}\sim \frac{|t|^{{\delta}-a} \prod_{i=1}^{r}|\alpha_i t+c_i|^{\alpha_i a+b_i}}{|t|^{{\delta}-a+{\rho}+1}\prod_{i=1}^{r}|\alpha_i t+c_i|^{\alpha_i {\delta}-\alpha_i a+b_i}},
\end{equation*}
\begin{equation*}
\frac{\Gamma(s)\prod_{i=1}^{r}\Gamma(\alpha_i({\delta}-s)+\bar{\beta}_i)}{\Gamma(s+{\rho}+1)\prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)}\sim \frac{|t|^{{\delta}-a} \prod_{i=1}^{r}|\alpha_i t+c_i|^{\alpha_i a+b_i}}{|t|^{{\delta}-a+{\rho}+1}\prod_{i=1}^{r}|\alpha_i t+c_i|^{\alpha_i {\delta}-\alpha_i a+b_i}},
\end{equation*} as ![]() $|t|\rightarrow \infty$. On simplifying, this gives
$|t|\rightarrow \infty$. On simplifying, this gives
 \begin{equation*}
f(s)\ll_{\boldsymbol \alpha,\boldsymbol \beta} |t|^{-{\rho}-1+(2a-{\delta}) \sum_{i=1}^{r}\alpha_i},
\end{equation*}
\begin{equation*}
f(s)\ll_{\boldsymbol \alpha,\boldsymbol \beta} |t|^{-{\rho}-1+(2a-{\delta}) \sum_{i=1}^{r}\alpha_i},
\end{equation*} which is o(1) provided  ${\rho} \gt (2a-{\delta})d_F^{'}-1$.
${\rho} \gt (2a-{\delta})d_F^{'}-1$.
Finally, in order to apply lemma 2.4, we need to bound f(s) inside the strip ![]() ${\delta}-a \leq \operatorname{Re}(s) \leq a$. Inside this strip, we may write f(s) as
${\delta}-a \leq \operatorname{Re}(s) \leq a$. Inside this strip, we may write f(s) as
 \begin{equation*}
f(s)=\frac{\Gamma(s) \chi(s) x^{s+\rho}}{\Gamma(s+\rho+1) \prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right) Q^s},
\end{equation*}
\begin{equation*}
f(s)=\frac{\Gamma(s) \chi(s) x^{s+\rho}}{\Gamma(s+\rho+1) \prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right) Q^s},
\end{equation*} where ![]() $\chi(s)$ is as in definition 1.1. As
$\chi(s)$ is as in definition 1.1. As  $\frac{1}{\Gamma(s)}$ is an analytic function of order 1, we have
$\frac{1}{\Gamma(s)}$ is an analytic function of order 1, we have
 \begin{equation*}
\frac{1}{\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)}= O\left(\exp\left(r|s|\right)\right).
\end{equation*}
\begin{equation*}
\frac{1}{\prod_{i=1}^r \Gamma\left(\alpha_i s+\beta_i \right)}= O\left(\exp\left(r|s|\right)\right).
\end{equation*}Combining this with (1.7) and (5.3), we have
 \begin{equation*}
f(s)\ll \exp\left(\exp\left(\frac{\theta \pi|s|}{2a-{\delta}}\right)\right),
\end{equation*}
\begin{equation*}
f(s)\ll \exp\left(\exp\left(\frac{\theta \pi|s|}{2a-{\delta}}\right)\right),
\end{equation*} uniformly for ![]() ${\delta}-a \leq \operatorname{Re}(s) \leq a$ as needed. We may now apply lemma 2.4 to conclude that the horizontal integrals in (5.2) vanish as
${\delta}-a \leq \operatorname{Re}(s) \leq a$ as needed. We may now apply lemma 2.4 to conclude that the horizontal integrals in (5.2) vanish as ![]() $T \rightarrow \infty$, provided
$T \rightarrow \infty$, provided  ${\rho} \gt \max{\{0, (2a-{\delta})d_F^{'}-1\}}$.
${\rho} \gt \max{\{0, (2a-{\delta})d_F^{'}-1\}}$.
Defining ![]() $Q_{\rho}(x)$ as in (1.14), we have thus obtained from (5.2),
$Q_{\rho}(x)$ as in (1.14), we have thus obtained from (5.2),
 \begin{align*}
& \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}f(s)ds\notag\\
& \quad =\frac{1}{2 \pi i}\int_{C} f(s) ds+ \frac{1}{2 \pi i}\int_{\delta-a-i\infty}^{\delta-a+i\infty} \frac{\phi(s)\Gamma(s) x^{s+\rho}}{\Gamma(s+\rho+1)}ds \\
& \quad =Q_\rho(x)+\frac{1}{2 \pi i}\int_{\delta-a-i\infty}^{\delta-a+i\infty} \frac{\Gamma(s) x^{s+\rho}\omega Q^{\delta-2s}\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\bar{\beta}_i)\overline{\psi(\delta-\bar{s})}}{\Gamma(s+\rho+1)\prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)}ds,
\end{align*}
\begin{align*}
& \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}f(s)ds\notag\\
& \quad =\frac{1}{2 \pi i}\int_{C} f(s) ds+ \frac{1}{2 \pi i}\int_{\delta-a-i\infty}^{\delta-a+i\infty} \frac{\phi(s)\Gamma(s) x^{s+\rho}}{\Gamma(s+\rho+1)}ds \\
& \quad =Q_\rho(x)+\frac{1}{2 \pi i}\int_{\delta-a-i\infty}^{\delta-a+i\infty} \frac{\Gamma(s) x^{s+\rho}\omega Q^{\delta-2s}\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\bar{\beta}_i)\overline{\psi(\delta-\bar{s})}}{\Gamma(s+\rho+1)\prod_{i=1}^{r}\Gamma(\alpha_is+\beta_i)}ds,
\end{align*} upon using the functional equation (1.9) and denoting the integral  $\frac{1}{2 \pi i}\int_{C} f(s) ds$ by
$\frac{1}{2 \pi i}\int_{C} f(s) ds$ by ![]() $Q_\rho(x)$. Changing the variable
$Q_\rho(x)$. Changing the variable ![]() $\delta-s$ to s on the right-hand side above, we get
$\delta-s$ to s on the right-hand side above, we get
 \begin{align}
& \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}f(s)ds \notag\\
& \quad = Q_\rho(x)+\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \frac{\Gamma(\delta-s) x^{\delta-s+\rho}\omega Q^{2s-\delta}\prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta}_i)\overline{\psi(\bar{s})}}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}ds.
\end{align}
\begin{align}
& \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty}f(s)ds \notag\\
& \quad = Q_\rho(x)+\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \frac{\Gamma(\delta-s) x^{\delta-s+\rho}\omega Q^{2s-\delta}\prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta}_i)\overline{\psi(\bar{s})}}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}ds.
\end{align} We will now justify the interchange of the integral and sum (coming from  $\overline{\psi(\bar{s})}=\sum_{n=1}^{\infty}\bar{b}_n\mu_n^{-s}$) on the right-hand side of the above expression as follows.
$\overline{\psi(\bar{s})}=\sum_{n=1}^{\infty}\bar{b}_n\mu_n^{-s}$) on the right-hand side of the above expression as follows.
Let us define
 \begin{equation*}
I_{\rho}\left(\frac{\mu_nx}{Q^2}\right):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta}_i)}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\left(\frac{\mu_nx}{Q^2}\right)^{{\delta}+{\rho}-s}ds
\end{equation*}
\begin{equation*}
I_{\rho}\left(\frac{\mu_nx}{Q^2}\right):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta}_i)}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\left(\frac{\mu_nx}{Q^2}\right)^{{\delta}+{\rho}-s}ds
\end{equation*}and
 \begin{equation*}
J_{\rho}(x):=\sum_{n=1}^{\infty}\bar{b}_n \frac{Q^{{\delta}+2{\rho}}}{\mu_n^{{\delta}+{\rho}}}I_{\rho}\left(\frac{\mu_nx}{Q^2}\right).
\end{equation*}
\begin{equation*}
J_{\rho}(x):=\sum_{n=1}^{\infty}\bar{b}_n \frac{Q^{{\delta}+2{\rho}}}{\mu_n^{{\delta}+{\rho}}}I_{\rho}\left(\frac{\mu_nx}{Q^2}\right).
\end{equation*} From lemma 2.11, we deduce as ![]() $x\rightarrow \infty$,
$x\rightarrow \infty$,
 \begin{align*}&I_\rho \left(\frac{\mu_nx}{Q^2}\right)\sim \left(\frac{\mu_nx}{Q^2}\right)^{\frac{d_F^{'}\delta+(2d_F^{'}-1)\rho-2i\nu-\frac{1}{2}}{2d_F^{'}}}\sum_{q=0}^{m} A_q \left(\frac{\mu_nx}{Q^2}\right)^{-\frac{q}{2d_F^{'}}}\nonumber\\
&\qquad \quad\cos\left(\left(\frac{\mu_nx}{hQ^2}\right)^\frac{1}{2d_F^{'}}+\pi\left(d_F^{'}\gamma+\frac{q}{2}+ i\nu- \mu\right)\right),\end{align*}
\begin{align*}&I_\rho \left(\frac{\mu_nx}{Q^2}\right)\sim \left(\frac{\mu_nx}{Q^2}\right)^{\frac{d_F^{'}\delta+(2d_F^{'}-1)\rho-2i\nu-\frac{1}{2}}{2d_F^{'}}}\sum_{q=0}^{m} A_q \left(\frac{\mu_nx}{Q^2}\right)^{-\frac{q}{2d_F^{'}}}\nonumber\\
&\qquad \quad\cos\left(\left(\frac{\mu_nx}{hQ^2}\right)^\frac{1}{2d_F^{'}}+\pi\left(d_F^{'}\gamma+\frac{q}{2}+ i\nu- \mu\right)\right),\end{align*} where Aq are some constants and ![]() $\nu, \mu, h$ are as defined in (2.17). Using this, we have
$\nu, \mu, h$ are as defined in (2.17). Using this, we have
 \begin{equation}
J_{\rho}(x)\ll \sum_{n=1}^{\infty}|b_n| \frac{Q^{{\delta}+2{\rho}}}{|\mu_n|^{{\delta}+{\rho}}} \left(\frac{|\mu_n|x}{Q^2}\right)^{\frac{d_F^{'}{\delta}+(2d_F^{'}-1){\rho}-\frac{1}{2}}{2d_F^{'}}}.
\end{equation}
\begin{equation}
J_{\rho}(x)\ll \sum_{n=1}^{\infty}|b_n| \frac{Q^{{\delta}+2{\rho}}}{|\mu_n|^{{\delta}+{\rho}}} \left(\frac{|\mu_n|x}{Q^2}\right)^{\frac{d_F^{'}{\delta}+(2d_F^{'}-1){\rho}-\frac{1}{2}}{2d_F^{'}}}.
\end{equation} As  $\sum_{n=1}^{\infty}\frac{b_n}{\mu_n^{s}}$ converges absolutely for
$\sum_{n=1}^{\infty}\frac{b_n}{\mu_n^{s}}$ converges absolutely for ![]() $\operatorname{Re}(s) \gt {\sigma}_b$, from (5.5) we deduce that
$\operatorname{Re}(s) \gt {\sigma}_b$, from (5.5) we deduce that ![]() $J_{\rho}(x)$ converges absolutely and uniformly in a compact domain for
$J_{\rho}(x)$ converges absolutely and uniformly in a compact domain for  ${\rho} \gt 2d_F^{'}{\sigma}_b-d_F^{'}{\delta}-\frac{1}{2}$. We thus interchange the order of summation and integration in (5.4). Finally combining this with (5.1) yields
${\rho} \gt 2d_F^{'}{\sigma}_b-d_F^{'}{\delta}-\frac{1}{2}$. We thus interchange the order of summation and integration in (5.4). Finally combining this with (5.1) yields
 \begin{align}
& \frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{\lambda_n \leqslant x}{} a_{n}(x-\lambda_n)^\rho \nonumber\\
& \quad =Q_\rho(x)+\frac{\omega x^{\delta+\rho}}{Q^\delta} \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \qquad \times \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta}_i)}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds,
\end{align}
\begin{align}
& \frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{\lambda_n \leqslant x}{} a_{n}(x-\lambda_n)^\rho \nonumber\\
& \quad =Q_\rho(x)+\frac{\omega x^{\delta+\rho}}{Q^\delta} \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \qquad \times \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta}_i)}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds,
\end{align} for ![]() ${\rho} \geq 0$ and
${\rho} \geq 0$ and  ${\rho} \gt (2a-{\delta})d_F^{'} -1$. However, we can differentiate the identity (5.6) with respect to x and extend the validity of the identity for smaller values of ρ, since differentiating with respect to x gives
${\rho} \gt (2a-{\delta})d_F^{'} -1$. However, we can differentiate the identity (5.6) with respect to x and extend the validity of the identity for smaller values of ρ, since differentiating with respect to x gives
 \begin{align*}
\frac{1}{\Gamma(\rho)}\sideset{}{'}\sum_{\lambda_n \leqslant x}{} a_{n}(x-\lambda_n)^{\rho-1}& =Q_{\rho-1}(x)+\frac{\omega x^{\delta+\rho-1}}{Q^\delta} \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \quad \times \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta_i)}}{\Gamma(\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds,
\end{align*}
\begin{align*}
\frac{1}{\Gamma(\rho)}\sideset{}{'}\sum_{\lambda_n \leqslant x}{} a_{n}(x-\lambda_n)^{\rho-1}& =Q_{\rho-1}(x)+\frac{\omega x^{\delta+\rho-1}}{Q^\delta} \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \quad \times \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_is+\bar{\beta_i)}}{\Gamma(\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds,
\end{align*} which is simply the identity (5.6) with ρ replaced by ![]() ${\rho}-1$. In order to justify this differentiation and to deduct how many times one can apply it repeatedly, we first observe that the series on the right-hand side of (5.6) is uniformly convergent for
${\rho}-1$. In order to justify this differentiation and to deduct how many times one can apply it repeatedly, we first observe that the series on the right-hand side of (5.6) is uniformly convergent for  ${\rho} \gt (2{\sigma}_b-{\delta})d_F^{'} -\frac{1}{2}$. Hence, for any
${\rho} \gt (2{\sigma}_b-{\delta})d_F^{'} -\frac{1}{2}$. Hence, for any  ${\rho} \gt (2{\sigma}_b-{\delta})d_F^{'} -\frac{1}{2}$, the right-hand side of (5.6) is continuously differentiable (since
${\rho} \gt (2{\sigma}_b-{\delta})d_F^{'} -\frac{1}{2}$, the right-hand side of (5.6) is continuously differentiable (since ![]() $Q_{\rho}(x)$ is
$Q_{\rho}(x)$ is ![]() $C^\infty$ from lemma 2.3). In particular, for any such value of ρ, the right-hand side of (5.6) is continuous. Since the values of an on the left-hand side of (5.6) are not all zero, for the left-hand sum to be continuous, we must have the exponent ρ > 0. We thus conclude that
$C^\infty$ from lemma 2.3). In particular, for any such value of ρ, the right-hand side of (5.6) is continuous. Since the values of an on the left-hand side of (5.6) are not all zero, for the left-hand sum to be continuous, we must have the exponent ρ > 0. We thus conclude that  $(2{\sigma}_b-{\delta})d_F^{'}-\frac{1}{2}$ must be non-negative. Since
$(2{\sigma}_b-{\delta})d_F^{'}-\frac{1}{2}$ must be non-negative. Since  $(2a-{\delta})d_F^{'}-1=(2{\sigma}_b-{\delta})d_F^{'}-\frac{1}{2}+m\geq m$, this means that (5.6) can be differentiated m times to yield the same identity for any
$(2a-{\delta})d_F^{'}-1=(2{\sigma}_b-{\delta})d_F^{'}-\frac{1}{2}+m\geq m$, this means that (5.6) can be differentiated m times to yield the same identity for any  ${\rho} \gt (2{\sigma}_b-{\delta})d_F^{'}-\frac{1}{2}$. This completes the proof.
${\rho} \gt (2{\sigma}_b-{\delta})d_F^{'}-\frac{1}{2}$. This completes the proof.
6. Proof of theorem 1.7
We first multiply the Riesz sum identity (1.13) throughout by
 \begin{equation*}
A(x):=y^{{\rho}+1} \frac{1}{2\pi i} \int_{k-i\infty}^{k+i\infty} \Gamma(s)\prod_{i=1}^{r}\Gamma\left(\alpha_i(s-{\rho}-1)+\beta_i\right) (xy)^{-s}ds,
\end{equation*}
\begin{equation*}
A(x):=y^{{\rho}+1} \frac{1}{2\pi i} \int_{k-i\infty}^{k+i\infty} \Gamma(s)\prod_{i=1}^{r}\Gamma\left(\alpha_i(s-{\rho}-1)+\beta_i\right) (xy)^{-s}ds,
\end{equation*} for a suitable k > 0 and then integrate with respect to x from 0 to ![]() $\infty$. We have
$\infty$. We have
 \begin{align}
&\frac{1}{\Gamma(\rho+1)}\int_{0}^{\infty}\sideset{}{'}\sum_{\lambda_n \leq x}{} a_{n}(x-\lambda_n)^\rho A(x)dx=\int_{0}^{\infty}Q_{\rho}(x)A(x)dx\nonumber\\
& \quad +\int_{0}^{\infty}\bigg(\frac{\omega x^{\delta+\rho}}{Q^\delta}\bigg) \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \quad \times \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_i s+\bar{\beta}_i)}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds A(x)dx \nonumber\\
&\quad =K_1(y)+K_2(y) \quad \text{(say).}
\end{align}
\begin{align}
&\frac{1}{\Gamma(\rho+1)}\int_{0}^{\infty}\sideset{}{'}\sum_{\lambda_n \leq x}{} a_{n}(x-\lambda_n)^\rho A(x)dx=\int_{0}^{\infty}Q_{\rho}(x)A(x)dx\nonumber\\
& \quad +\int_{0}^{\infty}\bigg(\frac{\omega x^{\delta+\rho}}{Q^\delta}\bigg) \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \quad \times \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_i s+\bar{\beta}_i)}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds A(x)dx \nonumber\\
&\quad =K_1(y)+K_2(y) \quad \text{(say).}
\end{align}Using the theory of the multiple Mellin integral [Reference Titchmarsh38, p. 53], it can be verified that
 \begin{equation}
A(x)=y^{{\rho}+1}\int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r)\frac{du_r}{u_r ^{{\rho}+2}} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1)f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) \frac{du_1}{u_1 ^{{\rho}+2}},
\end{equation}
\begin{equation}
A(x)=y^{{\rho}+1}\int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r)\frac{du_r}{u_r ^{{\rho}+2}} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1)f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) \frac{du_1}{u_1 ^{{\rho}+2}},
\end{equation} where ![]() $f_{\alpha_0, \beta_0}=\exp(-x)$ and
$f_{\alpha_0, \beta_0}=\exp(-x)$ and  $f_{\alpha_i, \beta_i}= \frac{\exp(-x^{1/\alpha_i})}{\alpha_i x^{\beta_i/\alpha_i}}$ for
$f_{\alpha_i, \beta_i}= \frac{\exp(-x^{1/\alpha_i})}{\alpha_i x^{\beta_i/\alpha_i}}$ for ![]() $i=1,\dots, r$. Further using lemma 2.9, we can deduce that
$i=1,\dots, r$. Further using lemma 2.9, we can deduce that
 \begin{equation}
A(x)\ll \exp{\Big(-c(xy)^{\frac{1}{1+d_F^{'}}}\Big)}.
\end{equation}
\begin{equation}
A(x)\ll \exp{\Big(-c(xy)^{\frac{1}{1+d_F^{'}}}\Big)}.
\end{equation}Now, the integral on the left-hand side of (6.1) converges absolutely due to the exponential decay of A(x). Hence, using (6.2) and interchanging the integration and summation, we obtain that
 \begin{align}
& \frac{1}{\Gamma(\rho+1)}\int_{0}^{\infty}\sideset{}{'}\sum_{\lambda_n \leq x}{} a_{n}(x-\lambda_n)
^\rho A(x)dx\notag\\
& \quad =\frac{y^{{\rho}+1}}{\Gamma({\rho}+1)} \sum_{n=1}^{\infty} a_{n} \int_{\lambda_n}^{\infty} \! \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) \frac{du_r}{u_r ^{{\rho}+2}} \notag\\
& \qquad \cdots \! \int_{0}^{\infty} \! \! f_{\alpha_1, \beta_1}(u_1)f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) \frac{du_1}{u_1 ^{{\rho}+2}}(x-\lambda_n)^{\rho} dx.
\end{align}
\begin{align}
& \frac{1}{\Gamma(\rho+1)}\int_{0}^{\infty}\sideset{}{'}\sum_{\lambda_n \leq x}{} a_{n}(x-\lambda_n)
^\rho A(x)dx\notag\\
& \quad =\frac{y^{{\rho}+1}}{\Gamma({\rho}+1)} \sum_{n=1}^{\infty} a_{n} \int_{\lambda_n}^{\infty} \! \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) \frac{du_r}{u_r ^{{\rho}+2}} \notag\\
& \qquad \cdots \! \int_{0}^{\infty} \! \! f_{\alpha_1, \beta_1}(u_1)f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) \frac{du_1}{u_1 ^{{\rho}+2}}(x-\lambda_n)^{\rho} dx.
\end{align}Again, due to the absolute convergence of the above, we use Fubini’s theorem to interchange the order of integration to see that the above expression equals
 \begin{align}
& \frac{y^{{\rho}+1}}{\Gamma({\rho}+1)} \sum_{n=1}^{\infty} a_{n} \! \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) \frac{du_r}{u_r ^{{\rho}+2}} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) \notag\\
& \quad \times \left[\int_{\lambda_n}^{\infty} f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) (x-\lambda_n)^{\rho} dx\right] \frac{du_1}{u_1 ^{{\rho}+2}}.
\end{align}
\begin{align}
& \frac{y^{{\rho}+1}}{\Gamma({\rho}+1)} \sum_{n=1}^{\infty} a_{n} \! \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) \frac{du_r}{u_r ^{{\rho}+2}} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) \notag\\
& \quad \times \left[\int_{\lambda_n}^{\infty} f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) (x-\lambda_n)^{\rho} dx\right] \frac{du_1}{u_1 ^{{\rho}+2}}.
\end{align}As ρ > 0, by the definition of the Gamma function, we have
 \begin{equation*}
\int_{\lambda_n}^{\infty} f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) (x-\lambda_n)^{\rho} dx= \Gamma({\rho}+1) \exp\left(\frac{-\lambda_ny}{u_1\cdots u_r}\right)\left(\frac{u_1 \cdots u_r}{y}\right)^{{\rho}+1}.
\end{equation*}
\begin{equation*}
\int_{\lambda_n}^{\infty} f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) (x-\lambda_n)^{\rho} dx= \Gamma({\rho}+1) \exp\left(\frac{-\lambda_ny}{u_1\cdots u_r}\right)\left(\frac{u_1 \cdots u_r}{y}\right)^{{\rho}+1}.
\end{equation*}Substituting this into (6.5), the left-hand side of (3.3) equals
 \begin{align*}
\sum_{n=1}^{\infty} a_{n} \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) \frac{du_r}{u_r} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) \exp\left(\frac{-ny}{u_1\cdots u_r}\right) \frac{du_1}{u_1}.
\end{align*}
\begin{align*}
\sum_{n=1}^{\infty} a_{n} \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) \frac{du_r}{u_r} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) \exp\left(\frac{-ny}{u_1\cdots u_r}\right) \frac{du_1}{u_1}.
\end{align*} The integral on the right-hand side above is simply ![]() $Y_{\boldsymbol\alpha,\boldsymbol\beta}(ny)$ of lemma 2.5, which yields the left-hand side of our auxiliary modular relation (1.17).
$Y_{\boldsymbol\alpha,\boldsymbol\beta}(ny)$ of lemma 2.5, which yields the left-hand side of our auxiliary modular relation (1.17).
We now try to derive the right-hand side of (1.17). The integral ![]() $K_1(y)$ (in (6.1)) is absolutely convergent as
$K_1(y)$ (in (6.1)) is absolutely convergent as ![]() $Q_{\rho}(x)$ is a function of the form
$Q_{\rho}(x)$ is a function of the form ![]() $\sum c_\alpha x^{\alpha}$ with finite number of terms and A(x) has exponential decay. Recalling the definition (1.14) of
$\sum c_\alpha x^{\alpha}$ with finite number of terms and A(x) has exponential decay. Recalling the definition (1.14) of ![]() $Q_{\rho}(x)$, we interchange the order of integration to see that
$Q_{\rho}(x)$, we interchange the order of integration to see that ![]() $K_1(y)$ is
$K_1(y)$ is
 \begin{align*}
& \frac{y^{{\rho}+1}}{2 \pi i} \! \int_{C} \! \frac{\phi(s)\Gamma(s) }{\Gamma(s+\rho+1)} ds \! \int_{0}^{\infty} \!\! f_{\alpha_r, \beta_r}(u_r) \frac{du_r}{u_r ^{{\rho}+2}} \cdots \! \int_{0}^{\infty}\!\! f_{\alpha_1, \beta_1}(u_1) \notag\\
& \quad \times\left[\int_{0}^{\infty} \!\! f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) x^{s+\rho} dx\right] \frac{du_1}{u_1 ^{{\rho}+2}}.
\end{align*}
\begin{align*}
& \frac{y^{{\rho}+1}}{2 \pi i} \! \int_{C} \! \frac{\phi(s)\Gamma(s) }{\Gamma(s+\rho+1)} ds \! \int_{0}^{\infty} \!\! f_{\alpha_r, \beta_r}(u_r) \frac{du_r}{u_r ^{{\rho}+2}} \cdots \! \int_{0}^{\infty}\!\! f_{\alpha_1, \beta_1}(u_1) \notag\\
& \quad \times\left[\int_{0}^{\infty} \!\! f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) x^{s+\rho} dx\right] \frac{du_1}{u_1 ^{{\rho}+2}}.
\end{align*}Again, since
 \begin{equation*}
\int_{0}^{\infty} f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) x^{s+\rho} dx = \Gamma(s+{\rho}+1) \left(\frac{u_1 \cdots u_r}{y}\right)^{s+{\rho}+1},
\end{equation*}
\begin{equation*}
\int_{0}^{\infty} f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) x^{s+\rho} dx = \Gamma(s+{\rho}+1) \left(\frac{u_1 \cdots u_r}{y}\right)^{s+{\rho}+1},
\end{equation*}we obtain
 \begin{equation*}
K_1(y)=\frac{1}{2 \pi i} \int_{C} \phi(s)\Gamma(s) \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) u_r ^{s-1} du_r \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) u_1 ^{s-1} du_1 y^{-s} ds.
\end{equation*}
\begin{equation*}
K_1(y)=\frac{1}{2 \pi i} \int_{C} \phi(s)\Gamma(s) \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) u_r ^{s-1} du_r \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) u_1 ^{s-1} du_1 y^{-s} ds.
\end{equation*} Recalling (2.1), it is evident that ![]() $K_1(y)$ is equal to
$K_1(y)$ is equal to ![]() $P_1(y)$, which is the first term on the right-hand side of the needed auxiliary modular relation (1.17).
$P_1(y)$, which is the first term on the right-hand side of the needed auxiliary modular relation (1.17).
We now turn to ![]() $K_2(y)$, which we will denote as K 2 for simplicity. By the bound (5.5), we have
$K_2(y)$, which we will denote as K 2 for simplicity. By the bound (5.5), we have
 \begin{equation*}
K_2\ll \int_{0}^{\infty} \bigg(\frac{\omega x^{\delta+\rho}}{Q^\delta}\bigg) \sum_{n=1}^{\infty}|b_n| \left(\frac{Q^2}{|\mu_n|x}\right)^{{\delta}+{\rho}} \left(\frac{|\mu_n|x}{Q^2}\right)^{\frac{d_F^{'}{\delta}+(2d_F^{'}-1){\rho}-\frac{1}{2}}{2d_F^{'}}} A(x)dx.
\end{equation*}
\begin{equation*}
K_2\ll \int_{0}^{\infty} \bigg(\frac{\omega x^{\delta+\rho}}{Q^\delta}\bigg) \sum_{n=1}^{\infty}|b_n| \left(\frac{Q^2}{|\mu_n|x}\right)^{{\delta}+{\rho}} \left(\frac{|\mu_n|x}{Q^2}\right)^{\frac{d_F^{'}{\delta}+(2d_F^{'}-1){\rho}-\frac{1}{2}}{2d_F^{'}}} A(x)dx.
\end{equation*} Here the series inside the above integral converges absolutely for  ${\rho} \gt (2{\sigma}_b-{\delta})d_F^{'}-\frac{1}{2}$ and thus K 2 converges absolutely due to (6.3). So we interchange the summation and integral to get
${\rho} \gt (2{\sigma}_b-{\delta})d_F^{'}-\frac{1}{2}$ and thus K 2 converges absolutely due to (6.3). So we interchange the summation and integral to get
 \begin{align*}
K_2 & =y^{{\rho}+1}\left(\frac{\omega }{Q^\delta}\right) \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i} \int_{0}^{\infty} \notag\\
& \!\!\quad \times \left[\int_{a-i\infty}^{a+i\infty} \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_i(s)+\bar{\beta_i)}}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds\right.
\\
& \!\!\quad \times \left.\int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r)\frac{du_r}{u_r ^{{\rho}+2}} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1)f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) \frac{du_1}{u_1 ^{{\rho}+2}} x^{\delta+\rho} \right]dx.
\end{align*}
\begin{align*}
K_2 & =y^{{\rho}+1}\left(\frac{\omega }{Q^\delta}\right) \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i} \int_{0}^{\infty} \notag\\
& \!\!\quad \times \left[\int_{a-i\infty}^{a+i\infty} \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_i(s)+\bar{\beta_i)}}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_nx}{Q^2}\bigg)^{-s}ds\right.
\\
& \!\!\quad \times \left.\int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r)\frac{du_r}{u_r ^{{\rho}+2}} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1)f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) \frac{du_1}{u_1 ^{{\rho}+2}} x^{\delta+\rho} \right]dx.
\end{align*}Again we use Fubini’s theorem to interchange the order of integration and obtain
 \begin{align*}
K_2 & =y^{{\rho}+1}\bigg(\frac{\omega }{Q^\delta}\bigg) \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i} \int_{a-i\infty}^{a+i\infty} \notag\\
& \quad \times \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_i(s)+\bar{\beta_i)}}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_n}{Q^2}\bigg)^{-s}ds \notag \\
& \quad \times \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r)\frac{du_r}{u_r ^{{\rho}+2}} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) \notag\\
& \quad \times \left[\int_{0}^{\infty}f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) x^{\delta+\rho-s} dx \right] \frac{du_1}{u_1 ^{{\rho}+2}}.
\end{align*}
\begin{align*}
K_2 & =y^{{\rho}+1}\bigg(\frac{\omega }{Q^\delta}\bigg) \sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i} \int_{a-i\infty}^{a+i\infty} \notag\\
& \quad \times \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_i(s)+\bar{\beta_i)}}{\Gamma(1+\delta-s+\rho)\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_n}{Q^2}\bigg)^{-s}ds \notag \\
& \quad \times \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r)\frac{du_r}{u_r ^{{\rho}+2}} \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) \notag\\
& \quad \times \left[\int_{0}^{\infty}f_{\alpha_0, \beta_0} \left(\frac{xy}{u_1u_2 \cdots u_r}\right) x^{\delta+\rho-s} dx \right] \frac{du_1}{u_1 ^{{\rho}+2}}.
\end{align*} The term inside the square brackets is  $\Gamma(1+\delta-s+{\rho}) \left(\frac{u_1 \cdots u_r}{y}\right)^{1+\delta-s+{\rho}} $, which gives
$\Gamma(1+\delta-s+{\rho}) \left(\frac{u_1 \cdots u_r}{y}\right)^{1+\delta-s+{\rho}} $, which gives
 \begin{align*}
K_2 & =\frac{\omega }{(Qy)^\delta}\sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i} \int_{a-i\infty}^{a+i\infty} \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_i(s)+\bar{\beta_i)}}{\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_n}{Q^2 y}\bigg)^{-s}ds \\
& \quad \times \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) u_r ^{\delta-s-1} du_r \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) u_1 ^{\delta-s-1} du_1 .
\end{align*}
\begin{align*}
K_2 & =\frac{\omega }{(Qy)^\delta}\sum_{n=1}^{\infty}\bar{b}_n\frac{1}{2 \pi i} \int_{a-i\infty}^{a+i\infty} \frac{\Gamma(\delta-s) \prod_{i=1}^{r}\Gamma(\alpha_i(s)+\bar{\beta_i)}}{\prod_{i=1}^{r}\Gamma(\alpha_i(\delta-s)+\beta_i)}\bigg(\frac{\mu_n}{Q^2 y}\bigg)^{-s}ds \\
& \quad \times \int_{0}^{\infty}f_{\alpha_r, \beta_r}(u_r) u_r ^{\delta-s-1} du_r \cdots \int_{0}^{\infty}f_{\alpha_1, \beta_1}(u_1) u_1 ^{\delta-s-1} du_1 .
\end{align*}We then use (2.1) to evaluate the integrals above and obtain the second term in the modular relation (1.17), which completes the proof of our theorem.
7. Proof of theorem 1.8
Since the proof is analogous to that of theorem 1.3, we only mention the main steps. Taking the Mellin transform of ![]() $Y_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)$, multiplying both sides by
$Y_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)$, multiplying both sides by ![]() $Q^s a_{n}$ and summing over n, we obtain
$Q^s a_{n}$ and summing over n, we obtain
 \begin{equation*}
Q^s \phi(s) \Gamma(s) \prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i)=Q^s \sum_{n=1}^{\infty} a_n \int_{0}^{\infty} Y_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_n x)x^{s-1} dx.
\end{equation*}
\begin{equation*}
Q^s \phi(s) \Gamma(s) \prod_{i=1}^{r} \Gamma(\alpha_i s+ \beta_i)=Q^s \sum_{n=1}^{\infty} a_n \int_{0}^{\infty} Y_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_n x)x^{s-1} dx.
\end{equation*}Using corollary 2.10, one can justify the exchange of summation and integration to get
 \begin{align}
Q^s \Gamma(s) F(s)&= Q^s\bigg( \int_{0}^{1} \sum_{n=1}^{\infty} a_n Y_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx+\int_{1}^{\infty} \sum_{n=1}^{\infty} a_n Y_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx\bigg) \nonumber\\
&=Q^s\bigg( \int_{0}^{1} P_1(x)x^{s-1} dx+\int_{1}^{\infty} \big(\Psi(x)x^{-s-1} dx+ \Phi(x)x^{s-1}\big) dx\bigg),
\end{align}
\begin{align}
Q^s \Gamma(s) F(s)&= Q^s\bigg( \int_{0}^{1} \sum_{n=1}^{\infty} a_n Y_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx+\int_{1}^{\infty} \sum_{n=1}^{\infty} a_n Y_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_nx)x^{s-1} dx\bigg) \nonumber\\
&=Q^s\bigg( \int_{0}^{1} P_1(x)x^{s-1} dx+\int_{1}^{\infty} \big(\Psi(x)x^{-s-1} dx+ \Phi(x)x^{s-1}\big) dx\bigg),
\end{align}on applying the modular relation (1.17). Note that here
 \begin{equation*}
\Phi(x)=\sum_{n=1}^{\infty} a_n Y_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_n x) \,\,\ \ \text{and} \ \ \,\, \Psi(x)= \frac{\omega x^\delta}{Q^\delta} \sum_{n=1}^{\infty} \bar{b}_n X_{\boldsymbol \alpha,\boldsymbol{\bar{\beta}}}\left(\frac{\mu_nx}{Q^2}\right).
\end{equation*}
\begin{equation*}
\Phi(x)=\sum_{n=1}^{\infty} a_n Y_{\boldsymbol \alpha,\boldsymbol\beta}(\lambda_n x) \,\,\ \ \text{and} \ \ \,\, \Psi(x)= \frac{\omega x^\delta}{Q^\delta} \sum_{n=1}^{\infty} \bar{b}_n X_{\boldsymbol \alpha,\boldsymbol{\bar{\beta}}}\left(\frac{\mu_nx}{Q^2}\right).
\end{equation*} We repeat this procedure for  $X_{\boldsymbol \alpha,\boldsymbol{\bar{\beta}}}\big(\frac{\mu_nx}{Q^2}\big)$ to obtain
$X_{\boldsymbol \alpha,\boldsymbol{\bar{\beta}}}\big(\frac{\mu_nx}{Q^2}\big)$ to obtain
 \begin{equation*}
\omega Q^s \overline{\psi(\bar{s})} \Gamma(\delta-s)\prod_{i=1}^{r} \Gamma(\alpha_i s+ \bar{\beta_i})
=\omega Q^{-s} \int_{0}^{\infty}\sum_{n=1}^{\infty} \bar{b}_n X_{\boldsymbol \alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_nx}{Q^2}\bigg)x^{s-1} dx.
\end{equation*}
\begin{equation*}
\omega Q^s \overline{\psi(\bar{s})} \Gamma(\delta-s)\prod_{i=1}^{r} \Gamma(\alpha_i s+ \bar{\beta_i})
=\omega Q^{-s} \int_{0}^{\infty}\sum_{n=1}^{\infty} \bar{b}_n X_{\boldsymbol \alpha,\boldsymbol{\bar{\beta}}}\bigg(\frac{\mu_nx}{Q^2}\bigg)x^{s-1} dx.
\end{equation*}Using the modular relation (1.17), we obtain
 \begin{align}
& \omega Q^s \Gamma(\delta-s) \overline{G(\bar{s})}\notag\\
& \quad = \omega Q^{-s}\bigg(\frac{Q^\delta}{\omega}\int_{0}^{1} \big(\Phi(1/x)-P_1(1/x)\big) x^{-\delta+s-1}+\frac{Q^\delta}{\omega}\int_{1}^{\infty}\sum_{n=1}^{\infty}\Psi(x)x^{-\delta+s-1} dx\bigg) \nonumber\\
& \quad =Q^{1-s}\left(-\int_{1}^{\infty}P_1(x)x^{\delta-s-1}dx+\int_{1}^{\infty}\big(\Psi(x)x^{-\delta+s-1}+\Phi(x)x^{\delta-s-1}\big)dx\right).
\end{align}
\begin{align}
& \omega Q^s \Gamma(\delta-s) \overline{G(\bar{s})}\notag\\
& \quad = \omega Q^{-s}\bigg(\frac{Q^\delta}{\omega}\int_{0}^{1} \big(\Phi(1/x)-P_1(1/x)\big) x^{-\delta+s-1}+\frac{Q^\delta}{\omega}\int_{1}^{\infty}\sum_{n=1}^{\infty}\Psi(x)x^{-\delta+s-1} dx\bigg) \nonumber\\
& \quad =Q^{1-s}\left(-\int_{1}^{\infty}P_1(x)x^{\delta-s-1}dx+\int_{1}^{\infty}\big(\Psi(x)x^{-\delta+s-1}+\Phi(x)x^{\delta-s-1}\big)dx\right).
\end{align} As done after (4.4), it can be checked that replacing s by ![]() ${\delta}-s$ in (7.2) makes it equal to (7.1). Thus, we have obtained
${\delta}-s$ in (7.2) makes it equal to (7.1). Thus, we have obtained
which gives the functional equation (1.9) since ![]() $\Gamma(s)$ does not vanish.
$\Gamma(s)$ does not vanish.
8. Special cases
Let us consider the generalized divisor function  ${\sigma}^{(k)}_z(n)$ defined for
${\sigma}^{(k)}_z(n)$ defined for ![]() $k \in \mathbb{N}$,
$k \in \mathbb{N}$, ![]() $z\in \mathbb{C}$ by
$z\in \mathbb{C}$ by
 \begin{equation*}
{\sigma}^{(k)}_z(n):=\sum_{d^k|n}d^z.
\end{equation*}
\begin{equation*}
{\sigma}^{(k)}_z(n):=\sum_{d^k|n}d^z.
\end{equation*} The Dirichlet series associated with  ${\sigma}^{(k)}_z(n)$ is given by
${\sigma}^{(k)}_z(n)$ is given by
 \begin{equation*}
\sum_{n=1}^{\infty}\frac{{\sigma}^{(k)}_z(n)}{n^s}=\zeta(s)\zeta(ks-z), \quad \operatorname{Re}(s) \gt \max\left\{1,\frac{1+\operatorname{Re}(z)}{k}\right\}.
\end{equation*}
\begin{equation*}
\sum_{n=1}^{\infty}\frac{{\sigma}^{(k)}_z(n)}{n^s}=\zeta(s)\zeta(ks-z), \quad \operatorname{Re}(s) \gt \max\left\{1,\frac{1+\operatorname{Re}(z)}{k}\right\}.
\end{equation*} It can be seen that ![]() $\zeta(ks-z)$ satisfies the functional equation
$\zeta(ks-z)$ satisfies the functional equation
 \begin{equation*}\pi^{-\frac{ks-z}{2}}\Gamma\left(\frac{sk-z}{2}\right)\zeta(ks-z)=\pi^{-\frac{(1-ks+z)}{2}}\Gamma\bigg(\frac{1-ks+z}{2}\bigg)\zeta(1-ks+z).\end{equation*}
\begin{equation*}\pi^{-\frac{ks-z}{2}}\Gamma\left(\frac{sk-z}{2}\right)\zeta(ks-z)=\pi^{-\frac{(1-ks+z)}{2}}\Gamma\bigg(\frac{1-ks+z}{2}\bigg)\zeta(1-ks+z).\end{equation*} Hence, we can say ![]() $\zeta(s)\zeta(ks-z)$ satisfies the functional equation
$\zeta(s)\zeta(ks-z)$ satisfies the functional equation
 \begin{align*}
& \pi^{-\frac{s}{2}-\frac{ks-z}{2}}\Gamma\bigg(\frac{s}{2}\bigg) \Gamma\bigg(\frac{ks-z}{2}\bigg)\zeta(s)\zeta(ks-z)\\ & \quad =\pi^{-\frac{(1-s)}{2}-\frac{(1-ks+z)}{2}}\Gamma\bigg(\frac{1-s}{2}\bigg) \Gamma\bigg(\frac{1-ks+z}{2}\bigg)\zeta(1-s)\zeta(1-ks+z),
\end{align*}
\begin{align*}
& \pi^{-\frac{s}{2}-\frac{ks-z}{2}}\Gamma\bigg(\frac{s}{2}\bigg) \Gamma\bigg(\frac{ks-z}{2}\bigg)\zeta(s)\zeta(ks-z)\\ & \quad =\pi^{-\frac{(1-s)}{2}-\frac{(1-ks+z)}{2}}\Gamma\bigg(\frac{1-s}{2}\bigg) \Gamma\bigg(\frac{1-ks+z}{2}\bigg)\zeta(1-s)\zeta(1-ks+z),
\end{align*} which is of the form (1.6) only if k = 1 and ![]() ${\delta}=z+1$ or if
${\delta}=z+1$ or if  $z=\frac{k-1}{2}$ and δ = 1. We discuss our main results for these two cases in the following examples.
$z=\frac{k-1}{2}$ and δ = 1. We discuss our main results for these two cases in the following examples.
Example 8.1. If we consider the case k = 1, our function can be denoted by ![]() ${\sigma}_z(n)$, defined as the sum of the
${\sigma}_z(n)$, defined as the sum of the ![]() $z{th}$ powers of the divisors of n. The associated Dirichlet series
$z{th}$ powers of the divisors of n. The associated Dirichlet series  $ \sum_{n=1}^{\infty} \frac{{\sigma}_z(n)}{n^s}$ satisfies
$ \sum_{n=1}^{\infty} \frac{{\sigma}_z(n)}{n^s}$ satisfies
 \begin{align}
& \pi^{-\frac{s}{2}-\frac{s-z}{2}}\Gamma\bigg(\frac{s}{2}\bigg) \Gamma\bigg(\frac{s-z}{2}\bigg)\zeta(s)\zeta(s-z)\notag\\
& \quad =\pi^{-\frac{(1-s)}{2}-\frac{(1-s+z)}{2}}\Gamma\bigg(\frac{1-s}{2}\bigg) \Gamma\bigg(\frac{1-s+z}{2}\bigg)\zeta(1-s)\zeta(1-s+z).
\end{align}
\begin{align}
& \pi^{-\frac{s}{2}-\frac{s-z}{2}}\Gamma\bigg(\frac{s}{2}\bigg) \Gamma\bigg(\frac{s-z}{2}\bigg)\zeta(s)\zeta(s-z)\notag\\
& \quad =\pi^{-\frac{(1-s)}{2}-\frac{(1-s+z)}{2}}\Gamma\bigg(\frac{1-s}{2}\bigg) \Gamma\bigg(\frac{1-s+z}{2}\bigg)\zeta(1-s)\zeta(1-s+z).
\end{align} Hence by taking  $a(n)=b(n)= \pi^{\frac{z}{2}}{\sigma}_z(n)$ and
$a(n)=b(n)= \pi^{\frac{z}{2}}{\sigma}_z(n)$ and ![]() $\lambda_n=\mu_n=n$, the functional equation (1.6) in definition 1.1 is satisfied for
$\lambda_n=\mu_n=n$, the functional equation (1.6) in definition 1.1 is satisfied for ![]() ${\delta}=z+1$,
${\delta}=z+1$, ![]() $Q=\pi^{-1}$, ω=1, and r = 2, with
$Q=\pi^{-1}$, ω=1, and r = 2, with  $\alpha_1=\frac{1}{2}$,
$\alpha_1=\frac{1}{2}$, ![]() $\beta_1=0$,
$\beta_1=0$,  $\alpha_2=\frac{1}{2}$, and
$\alpha_2=\frac{1}{2}$, and ![]() $\beta_2= -\frac{z}{2}$. We consider the various identities that our results are concerned with in the case of this Dirichlet series.
$\beta_2= -\frac{z}{2}$. We consider the various identities that our results are concerned with in the case of this Dirichlet series.
For ![]() $x,a \gt 0$, from theorem 1.2, we have
$x,a \gt 0$, from theorem 1.2, we have
 \begin{equation}
\sum_{n=1}^{\infty}\pi^{\frac{z}{2}}{\sigma}_z(n)Z_{\boldsymbol \alpha,\boldsymbol\beta}(nx)=P(x)+\left(\frac{\pi}{x}\right)^{z+1}\sum_{n=1}^{\infty}\pi^{\frac{z}{2}}\bar{{\sigma}}_z(n) Z_{\boldsymbol\alpha,\boldsymbol{\beta}}\bigg(\frac{n\pi^2}{x}\bigg),
\end{equation}
\begin{equation}
\sum_{n=1}^{\infty}\pi^{\frac{z}{2}}{\sigma}_z(n)Z_{\boldsymbol \alpha,\boldsymbol\beta}(nx)=P(x)+\left(\frac{\pi}{x}\right)^{z+1}\sum_{n=1}^{\infty}\pi^{\frac{z}{2}}\bar{{\sigma}}_z(n) Z_{\boldsymbol\alpha,\boldsymbol{\beta}}\bigg(\frac{n\pi^2}{x}\bigg),
\end{equation}where
 \begin{equation*}Z_{\boldsymbol \alpha,\boldsymbol\beta}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma\bigg(\frac{s}{2}\bigg) \Gamma\bigg(\frac{s-z}{2}\bigg) x^{-s}ds,\end{equation*}
\begin{equation*}Z_{\boldsymbol \alpha,\boldsymbol\beta}(x):=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma\bigg(\frac{s}{2}\bigg) \Gamma\bigg(\frac{s-z}{2}\bigg) x^{-s}ds,\end{equation*}and
 \begin{equation*}
P(x)= \frac{1}{2 \pi i}\int_{C}\pi^{\frac{z}{2}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right)\zeta(s)\zeta(s-z) x^{-s}ds,
\end{equation*}
\begin{equation*}
P(x)= \frac{1}{2 \pi i}\int_{C}\pi^{\frac{z}{2}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right)\zeta(s)\zeta(s-z) x^{-s}ds,
\end{equation*} with C denoting a circle of finite radius, encircling poles of the above integrand. Let x > 0 and  $\rho \gt 2{\sigma}-z-\frac{3}{2}$, where
$\rho \gt 2{\sigma}-z-\frac{3}{2}$, where ![]() ${\sigma}=\max\{1,1+\operatorname{Re}(z)\}$. Let
${\sigma}=\max\{1,1+\operatorname{Re}(z)\}$. Let ![]() $a \gt \max\{1,1+\operatorname{Re}(z)\}$ be sufficiently large so that all the singularities of
$a \gt \max\{1,1+\operatorname{Re}(z)\}$ be sufficiently large so that all the singularities of  $\pi^{\frac{z}{2}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right)\zeta(s)\zeta(s-z)$ are contained in the strip
$\pi^{\frac{z}{2}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right)\zeta(s)\zeta(s-z)$ are contained in the strip ![]() $z+1-a \lt \operatorname{Re}(s) \lt a$. Then, theorem 1.4 gives the Riesz-sum identity
$z+1-a \lt \operatorname{Re}(s) \lt a$. Then, theorem 1.4 gives the Riesz-sum identity
 \begin{align}
& \frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{n\leq x}{} \pi^{\frac{z}{2}}{\sigma}_z(n)(x-n)^\rho\notag\\
& \quad =Q_\rho(x)+ x^{z+1+\rho} \pi^{z+1}\sum_{n=1}^{\infty}\pi^{\frac{z}{2}}\bar{{\sigma}}_z(n)\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \qquad \times \frac{\Gamma(z+1-s) \Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right)}{\Gamma(z-s+\rho)\Gamma\left(\frac{1-s}{2}\right) \Gamma\left(\frac{1-s+z}{2}\right)}(nx\pi^2)^{-s}ds ,
\end{align}
\begin{align}
& \frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{n\leq x}{} \pi^{\frac{z}{2}}{\sigma}_z(n)(x-n)^\rho\notag\\
& \quad =Q_\rho(x)+ x^{z+1+\rho} \pi^{z+1}\sum_{n=1}^{\infty}\pi^{\frac{z}{2}}\bar{{\sigma}}_z(n)\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \qquad \times \frac{\Gamma(z+1-s) \Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right)}{\Gamma(z-s+\rho)\Gamma\left(\frac{1-s}{2}\right) \Gamma\left(\frac{1-s+z}{2}\right)}(nx\pi^2)^{-s}ds ,
\end{align}where
 \begin{equation*}
Q_\rho(x)=\frac{1}{2 \pi i}\int_{C}\frac{\pi^{\frac{z}{2}}\zeta(s)\zeta(s-z)\Gamma(s)x^{s+\rho}}{\Gamma(s+\rho+1)} ds,\nonumber
\end{equation*}
\begin{equation*}
Q_\rho(x)=\frac{1}{2 \pi i}\int_{C}\frac{\pi^{\frac{z}{2}}\zeta(s)\zeta(s-z)\Gamma(s)x^{s+\rho}}{\Gamma(s+\rho+1)} ds,\nonumber
\end{equation*} with ![]() $C=C_a$ denoting a circle of finite radius, lying inside the strip
$C=C_a$ denoting a circle of finite radius, lying inside the strip ![]() $z+1-a \lt \operatorname{Re}(s) \lt a$, containing all the singularities of
$z+1-a \lt \operatorname{Re}(s) \lt a$, containing all the singularities of  $\pi^{\frac{z}{2}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right)\zeta(s)\zeta(s-z)$, such that all the singularities of
$\pi^{\frac{z}{2}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right)\zeta(s)\zeta(s-z)$, such that all the singularities of  $\pi^{\frac{z}{2}}\zeta(s)\zeta(s-z)\Gamma(s)x^{s+\rho}$ which lie in this strip are contained inside C.
For the choices of a and C defined above, the following modular-type relation can be obtained from theorem 1.7,
$\pi^{\frac{z}{2}}\zeta(s)\zeta(s-z)\Gamma(s)x^{s+\rho}$ which lie in this strip are contained inside C.
For the choices of a and C defined above, the following modular-type relation can be obtained from theorem 1.7,
 \begin{align}
& \sum_{n=1}^{\infty}\pi^{\frac{z}{2}}{\sigma}_z(n)\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right) (nx)^{-s}=
P_1(x)\notag\\
& \quad +\left(\frac{\pi}{x}\right)\sum_{n=1}^{\infty}\pi^{\frac{z}{2}}\bar{{\sigma}}_z(n) \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(z+1-s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right) \left(\frac{n\pi^2}{x}\right)^{-s}ds,
\end{align}
\begin{align}
& \sum_{n=1}^{\infty}\pi^{\frac{z}{2}}{\sigma}_z(n)\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right) (nx)^{-s}=
P_1(x)\notag\\
& \quad +\left(\frac{\pi}{x}\right)\sum_{n=1}^{\infty}\pi^{\frac{z}{2}}\bar{{\sigma}}_z(n) \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(z+1-s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right) \left(\frac{n\pi^2}{x}\right)^{-s}ds,
\end{align}where
 \begin{equation*}
P_1(x)= \frac{1}{2 \pi i}\int_{C} \pi^{\frac{z}{2}}\Gamma(s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right)\zeta(s)\zeta(s-z)x^{-s}ds.
\end{equation*}
\begin{equation*}
P_1(x)= \frac{1}{2 \pi i}\int_{C} \pi^{\frac{z}{2}}\Gamma(s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{s-z}{2}\right)\zeta(s)\zeta(s-z)x^{-s}ds.
\end{equation*}By corollary 1.9, the relations (8.1), (8.2), (8.3), and (8.4) are equivalent.
Remark 8.2. If we take z to be an odd integer, the Gamma factors in the functional equation (8.1) can be reduced to a single Gamma factor using Legendre’s multiplication formula. In this case, the equivalence of the above identities follows directly from the work of Chandrasekharan and Narasimhan [Reference Chandrasekharan and Narasimhan17], which applies in the case of a single Gamma factor.
Example 8.3. Consider  $z=\frac{k-1}{2}$. Then the Dirichlet series associated with the arithmetical function
$z=\frac{k-1}{2}$. Then the Dirichlet series associated with the arithmetical function  ${\sigma}^{(k)}_{\frac{k-1}{2}}(n)$ satisfies the functional equation
${\sigma}^{(k)}_{\frac{k-1}{2}}(n)$ satisfies the functional equation
 \begin{align*}
& \pi^{\frac{k-1}{4}-\frac{k+1}{2}s}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)\\
& \quad =\pi^{-\frac{(k+3)}{4}+\frac{(k+1)}{2}s}\Gamma\left(\frac{1-s}{2}\right) \Gamma\left(\frac{-ks}{2}+\frac{k+1}{4}\right)\zeta(1-s)\zeta\left(-ks+\frac{k+1}{2}\right).
\end{align*}
\begin{align*}
& \pi^{\frac{k-1}{4}-\frac{k+1}{2}s}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)\\
& \quad =\pi^{-\frac{(k+3)}{4}+\frac{(k+1)}{2}s}\Gamma\left(\frac{1-s}{2}\right) \Gamma\left(\frac{-ks}{2}+\frac{k+1}{4}\right)\zeta(1-s)\zeta\left(-ks+\frac{k+1}{2}\right).
\end{align*} It can be seen by taking  $a_n=b_n= \pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n)$ and
$a_n=b_n= \pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n)$ and ![]() $\lambda_n=\mu_n=n$ that the functional equation (1.6) given in definition 1.1 is satisfied for δ = 1,
$\lambda_n=\mu_n=n$ that the functional equation (1.6) given in definition 1.1 is satisfied for δ = 1,  $Q=\pi^{-\frac{k+1}{2}}$, ω=1, and r = 2 with
$Q=\pi^{-\frac{k+1}{2}}$, ω=1, and r = 2 with  $\alpha_1=\frac{1}{2}$,
$\alpha_1=\frac{1}{2}$, ![]() $\beta_1=0$,
$\beta_1=0$,  $\alpha_2=\frac{k}{2}$, and
$\alpha_2=\frac{k}{2}$, and  $\beta_2= -\frac{k-1}{4}$.
$\beta_2= -\frac{k-1}{4}$.
For ![]() $x,a \gt 0$, theorem 1.2 gives
$x,a \gt 0$, theorem 1.2 gives
 \begin{equation}
\sum_{n=1}^{\infty}\pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n)Z_{\boldsymbol\alpha,\boldsymbol\beta}(nx)=P(x)+\left(\frac{\pi^{\frac{k+1}{2}}}{x}\right)\sum_{n=1}^{\infty}\pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n) Z_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\left(\frac{n\pi^{k+1}}{x}\right),
\end{equation}
\begin{equation}
\sum_{n=1}^{\infty}\pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n)Z_{\boldsymbol\alpha,\boldsymbol\beta}(nx)=P(x)+\left(\frac{\pi^{\frac{k+1}{2}}}{x}\right)\sum_{n=1}^{\infty}\pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n) Z_{\boldsymbol\alpha,\boldsymbol{\bar{\beta}}}\left(\frac{n\pi^{k+1}}{x}\right),
\end{equation}where
 \begin{equation*}Z_{\boldsymbol \alpha,\boldsymbol\beta}(x)=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right) x^{-s}ds,\end{equation*}
\begin{equation*}Z_{\boldsymbol \alpha,\boldsymbol\beta}(x)=\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right) x^{-s}ds,\end{equation*}and
 \begin{equation*}
P(x)= \frac{1}{2 \pi i}\int_{C}\pi^{\frac{k-1}{4}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)x^{-s}ds,
\end{equation*}
\begin{equation*}
P(x)= \frac{1}{2 \pi i}\int_{C}\pi^{\frac{k-1}{4}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)x^{-s}ds,
\end{equation*} with C denoting a circle of finite radius, encircling poles of the above integrand. Let x > 0,  $\rho \gt \frac{k}{2}$ and a > 1 be sufficiently large so that all the singularities of
$\rho \gt \frac{k}{2}$ and a > 1 be sufficiently large so that all the singularities of  $\pi^{\frac{k-1}{4}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)$ are contained in the strip
$\pi^{\frac{k-1}{4}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)$ are contained in the strip ![]() $1-a \lt \operatorname{Re}(s) \lt a$. From theorem 1.4, we obtain the Riesz-sum identity
$1-a \lt \operatorname{Re}(s) \lt a$. From theorem 1.4, we obtain the Riesz-sum identity
 \begin{align}
& \frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{n\leq x}{} \pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n)(x-n)^\rho\notag\\
& \quad =Q_\rho(x)+ x^{1+\rho} \pi^{\frac{k+1}{2}}\sum_{n=1}^{\infty}\pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n)\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \quad \times \frac{\Gamma(1-s) \Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)}{\Gamma(2-s+\rho)\Gamma\left(\frac{1-s}{2}\right) \Gamma\left(\frac{-ks}{2}+\frac{k+1}{4}\right)}(nx\pi^{k+1})^{-s}ds,
\end{align}
\begin{align}
& \frac{1}{\Gamma(\rho+1)}\sideset{}{'}\sum_{n\leq x}{} \pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n)(x-n)^\rho\notag\\
& \quad =Q_\rho(x)+ x^{1+\rho} \pi^{\frac{k+1}{2}}\sum_{n=1}^{\infty}\pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n)\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \quad \times \frac{\Gamma(1-s) \Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)}{\Gamma(2-s+\rho)\Gamma\left(\frac{1-s}{2}\right) \Gamma\left(\frac{-ks}{2}+\frac{k+1}{4}\right)}(nx\pi^{k+1})^{-s}ds,
\end{align}where
 \begin{equation*}
Q_\rho(x)=\frac{1}{2 \pi i}\int_{C}\frac{\pi^{\frac{k-1}{4}}\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)\Gamma(s)x^{s+\rho}}{\Gamma(s+\rho+1)} ds,\nonumber
\end{equation*}
\begin{equation*}
Q_\rho(x)=\frac{1}{2 \pi i}\int_{C}\frac{\pi^{\frac{k-1}{4}}\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)\Gamma(s)x^{s+\rho}}{\Gamma(s+\rho+1)} ds,\nonumber
\end{equation*} with ![]() $C=C_a$ denoting a circle of finite radius, lying inside the strip
$C=C_a$ denoting a circle of finite radius, lying inside the strip ![]() $1-a \lt \operatorname{Re}(s) \lt a$, containing all the singularities of
$1-a \lt \operatorname{Re}(s) \lt a$, containing all the singularities of  $\pi^{\frac{k-1}{4}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)$, such that all the singularities of
$\pi^{\frac{k-1}{4}}\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)$, such that all the singularities of  $\pi^{\frac{k-1}{4}}\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)\Gamma(s)x^{s+\rho}$ which lie in this strip are contained inside C. For the choices of a and C defined above, theorem 1.7 gives another modular-type relation
$\pi^{\frac{k-1}{4}}\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right)\Gamma(s)x^{s+\rho}$ which lie in this strip are contained inside C. For the choices of a and C defined above, theorem 1.7 gives another modular-type relation
 \begin{align}
& \sum_{n=1}^{\infty}\pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n)\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right) (nx)^{-s}=
P_1(x)\notag\\
& \quad +\left(\frac{\pi^{\frac{k+1}{2}}}{x}\right)\sum_{n=1}^{\infty}\pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n) \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \quad \times \Gamma(1-s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right) \left(\frac{n\pi^{k+1}}{x}\right)^{-s}ds,
\end{align}
\begin{align}
& \sum_{n=1}^{\infty}\pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n)\frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \Gamma(s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right) (nx)^{-s}=
P_1(x)\notag\\
& \quad +\left(\frac{\pi^{\frac{k+1}{2}}}{x}\right)\sum_{n=1}^{\infty}\pi^{\frac{k-1}{4}}{\sigma}^{(k)}_{\frac{k-1}{2}}(n) \frac{1}{2 \pi i}\int_{a-i\infty}^{a+i\infty} \notag\\
& \quad \times \Gamma(1-s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right) \left(\frac{n\pi^{k+1}}{x}\right)^{-s}ds,
\end{align}where
 \begin{equation*}
P_1(x)= \frac{1}{2 \pi i}\int_{C} \pi^{\frac{k-1}{4}}\Gamma(s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right) x^{-s}ds.
\end{equation*}
\begin{equation*}
P_1(x)= \frac{1}{2 \pi i}\int_{C} \pi^{\frac{k-1}{4}}\Gamma(s)\Gamma\left(\frac{s}{2}\right) \Gamma\left(\frac{ks}{2}-\frac{k-1}{4}\right)\zeta(s)\zeta\left(ks-\frac{k-1}{2}\right) x^{-s}ds.
\end{equation*}By corollary 1.9, the relations (8.1), (8.5), (8.6), and (8.7) are equivalent.
Example 8.4. The class of L-functions introduced by Selberg [Reference Selberg37] satisfies the hypothesis of definition 1.1 with δ = 1. This class, called the Selberg class, includes well-known L-functions such as the Dirichlet L-functions, Hecke L-functions associated with algebraic number fields, the Hecke L-functions associated with holomorphic modular forms under appropriate restrictions and normalizations, Artin L-functions under the assumption of the Artin conjecture, and the automorphic L-functions provided the Ramanujan conjecture holds. Our main result on the equivalence of functional equation, modular relation, and Riesz sum identity applies to this broad class of L-functions.
Acknowledgements
The third author was partially supported by the DST INSPIRE Faculty Award Program DST/ INSPIRE/Faculty/Batch-13/2018. Some of this work was carried out when the third author was visiting the Harish-Chandra Research Institute, Prayagraj and she is grateful for the kind hospitality.