Talcing into account vacuum polarization effects and a coherent massive scalar field we consider a singularity free cosmological model from which an intermediate inflationary stage follows quite naturally. According to the ideas of Tryon, Fomin, Zeldovich and others on the spontaneous creation of an universe by a quantum process the newly created universe must be closed. Its evolution starts from a finite initial value a of the order of the Planck length with a zero velocity ho = 0 (h - Hubble parameter). Therefore, in this moment an effective source term not fulfilling the strong energy condition must be dominant. It can originate fron a coherent massive scalar field (mass m) with zero kinetic energy 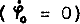and/or the vacuum polarization (considered here in the form of a modified gravitational Lagrangian with quadratic terms of the Ricci scalar). The corresponding general Lagrangian reads (c = h =1) 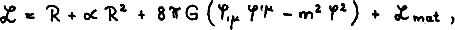where ∝ is a negative coupling constant and Lmat is the Lagrangian of other possible existing matter. Both the massive scalar field and the vacuum polarization effects drive the universe to expand exponentially for a definite time interval depending on the initial radius a0 and the parameters m and ∝, during which all other matter being originally present is diluted. The following small oscillations superimposed on the dust-like power law behaviour of the scale factor cause an intensive particle production, and the universe heats up to a radiation dominated Friedmann universe. This process must terminate before baryogenesis. The matching of the different phases of the cosmological evolution and the requirement to fit the parameters of the observed universe lead to a definite parameter range for m and |∝| well below the Planck values. In consequence the present mass density must be equal to the critical one (Ω = 1) with high accuracy.