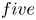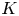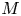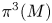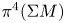1. Introduction
One of the goals of algebraic topology of manifolds is to determine the homotopy type of the (reduced) suspension space $\Sigma M$
of a given manifold M. This problem has attracted a lot of attention since So and Theriault's work [Reference So and Theriault21], which showed how the homotopy decompositions of the (double) suspension spaces of manifolds can be used to characterize some important invariants in geometry and mathematical physics, such as reduced $K$
-groups and gauge groups. Several works have followed this direction, such as [Reference Cutler and So7, Reference Huang9–Reference Huang and Li12, Reference Li15]. The integral homology groups $H_\ast (M)$
serve as the fundamental input for this topic. As shown by these papers, the 2-torsion of $H_\ast (M)$
and potential obstructions from certain Whitehead products usually prevent a complete homotopy classification of the (double) suspension space of a given manifold $M$
.
The main purpose of this paper is to investigate the homotopy types of the suspension of a non-simply-connected orientable closed smooth $five$
-manifold. Notice that Huang [Reference Huang9] studied the suspension homotopy of $five$
-manifolds $M$
that are $S^1$
-principal bundles over a simply-connected oriented closed $four$
-manifold. The homotopy decompositions of $\Sigma ^2M$
are successfully applied to determine the homotopy types of the pointed looped spaces of the gauge groups of a principal bundle over $M$
. In this paper we greatly loosen the restriction on the homology groups $H_\ast (M)$
of the non-simply-connected $five$
-manifold $M$
by assuming that $H_1(M)$
has a torsion subgroup that is not divided by $6$
and $H_2(M)$
contains a general torsion part.
To state our main results, we need the following notion and notations. Let $n\geq 2$
. Denote by $\eta =\eta _n=\Sigma ^{n-2}\eta$
the iterated suspension of the first Hopf map $\eta \colon S^3\to S^2$
. Recall from (cf. [Reference Toda25]) that $\pi _3(S^2)\cong {\mathbb {Z}}\langle \eta \rangle$
, $\pi _{n+1}(S^n)\cong {\mathbb {Z}/2^{}}\langle \eta \rangle$
for $n\geq 3$
and $\pi _{n+2}(S^n)\cong {\mathbb {Z}/2^{}}\langle \eta ^2 \rangle$
. For an abelian group $G$
, denote by $P^{n+1}(G)$
the Peterson space characterized by having a unique reduced cohomology group $G$
in dimension $n+1$
; in particular, denote by $P^{n+1}(k)=P^{n+1}( {\mathbb {Z}}/k)$
the mod $k$
Moore space of dimension $n+1$
, where ${\mathbb {Z}}/k$
is the group of integers modulo $k$
, $k\geq 2$
. There is a canonical homotopy cofibration
where $i_n$
is the inclusion of the bottom cell and $q_{n+1}$
is the pinch map to the top cell. Recall that for each prime $p$
and integer $r\geq 1$
, there are higher order Bockstein operations $\beta _r$
that detect the degree $2^r$
map on spheres $S^n$
. For each $r\geq 1$
, there are canonical maps $\tilde {\eta }_r\colon S^{n+2}\to P^{n+2}(2^r)$
satisfying the relation $q_{n+1}\tilde {\eta }_r=\eta$
, see lemma 2.2. A finite CW-complex $X$
is called an ${\mathbf {A}_{n}^{2}}$
-complex if it is $(n-1)$
-connected and has dimension at most $n+2$
. In 1950, Chang [Reference Chang4] proved that for $n\geq 3$
, every ${\mathbf {A}_{n}^{2}}$
-complex $X$
is homotopy equivalent to a wedge sum of finitely many spheres and mod $p^r$
Moore spaces with $p$
any primes and the following four elementary (or indecomposable) Chang complexes:
where $\boldsymbol {C}X$
denotes the reduced cone on $X$
and $r,\,s$
are positive integers. We recommend [Reference Li14, Reference Zhu, Li and Pan26–Reference Zhu and Pan29] for recent work on the homotopy theory of Chang complexes.
Now it is prepared to state our main result. Let $M$
be an orientable closed $five$
-manifold whose integral homology groups are given by
where $l,\,d$
are positive integers and $H,\,T$
are finitely generated torsion abelian groups.
Theorem 1.1 Let $M$
be an orientable smooth closed $five$
-manifold with $H_\ast (M)$
given by (1.1). Let $T_2\cong \bigoplus _{j=1}^{t_2} {\mathbb {Z}/2^{r_j}}$
be the $2$
-primary component of $T$
and suppose that $H$
contains no $2$
- or $3$
-torsion. There exist integers $c_1,\,c_2$
that depend on $M$
and satisfy
and $c_1=c_2=0$
if and only if the Steenrod square $\operatorname {Sq}^2$
acts trivially on $H^2(M; {\mathbb {Z}/2^{}})$
. Denote $T[c_2]=T/\oplus _{j=1}^{c_2} {\mathbb {Z}/2^{r_j}}$
.
(1) Suppose $M$
is spin, then there is a homotopy equivalence
\begin{align*} & \Sigma M\simeq \left(\bigvee_{i=1}^lS^2\right)\vee \left(\bigvee_{i=1}^{d-c_1}S^3\right)\vee \left(\bigvee_{i=1}^{d}S^4\right)\vee \left(\bigvee_{i=1}^{l-c_1-c_2}S^5\right)\vee P^3(H)\vee P^5(H)\\ & \quad \vee \left(\bigvee_{i=1}^{c_1} C^5_\eta\right)\vee P^4(T[c_2])\vee\left(\bigvee_{j=1}^{c_2}C^5_{r_j}\right)\vee S^6. \end{align*}
(2) Suppose $M$
is non-spin, then there are three possibilities for the homotopy types of $\Sigma M$.
(a) If for any $u,\, v\in H^4(\Sigma M; {\mathbb {Z}/2^{}})$
satisfying $\operatorname {Sq}^2(u)\neq 0$ and $\operatorname {Sq}^2(v)=0$, there holds $u+v\notin \operatorname {im}(\beta _r)$ for any $r\geq 1$, then there is a homotopy equivalence
\begin{align*} & \Sigma M\simeq \left(\bigvee_{i=1}^lS^2\right)\vee \left(\bigvee_{i=1}^{d-c_1}S^3\right)\vee \left(\bigvee_{i=2}^{d}S^4\right)\\ & \quad \vee \left(\bigvee_{i=1}^{l-c_1-c_2}S^5\right)\vee P^3(H)\vee P^5(H)\\ & \quad \vee \left(\bigvee_{i=1}^{c_1} C^5_\eta\right)\vee P^4(T[c_2])\vee\left(\bigvee_{j=1}^{c_2}C^5_{r_j}\right)\vee C^6_\eta; \end{align*}
(b) otherwise either there is a homotopy equivalence
\begin{align*} & \Sigma M\simeq \left(\bigvee_{i=1}^lS^2\right) \vee \left(\bigvee_{i=1}^{d-c_1}S^3\right)\vee \left(\bigvee_{i=1}^{d}S^4\right)\\ & \quad \vee \left(\bigvee_{i=1}^{l-c_1-c_2}S^5\right) \vee P^3(H)\vee P^5(H)\\ & \quad \vee \left(\bigvee_{i=1}^{c_1} C^5_\eta\right)\vee\left(\bigvee_{j=1}^{c_2}C^5_{r_j}\right)\vee P^4 \left(\frac{T[c_2]}{{\mathbb{Z}/2^{r_{j_1}}}}\right) \vee (P^4(2^{r_{j_1}})\cup_{\tilde{\eta}_{r_{j_1}}}\,{\rm e}^6), \end{align*}or there is a homotopy equivalence
\begin{align*} & \Sigma M\simeq \left(\bigvee_{i=1}^lS^2\right)\vee \left(\bigvee_{i=1}^{d-c_1}S^3\right)\vee \left(\bigvee_{i=1}^{d}S^4\right)\\ & \quad \vee \left(\bigvee_{i=1}^{l-c_1-c_2}S^5\right)\vee P^3(H)\vee P^5(H)\\ & \quad\vee \left(\bigvee_{i=1}^{c_1} C^5_\eta\right)\vee P^4(T[c_2])\vee\left(\bigvee_{j_1\neq j=1}^{c_2}C^5_{r_j}\right)\vee (C^5_{r_{j_1}}\cup_{i_P\tilde{\eta}_{r_{j_1}}}\,{\rm e}^6), \end{align*}where $i_P\colon P^{5}(2^{r_{j_1}})\to C^{6}_{r_{j_1}}$
is the canonical inclusion map; in both cases, $r_{j_1}$ is the minimum of $r_j$ such that $u+v\in \operatorname {im}(\beta _{r_{j_1}})$.
In Theorem 1.1 we characterize the homotopy types of $\Sigma M$
by elementary complexes of dimension at most six, up to certain indeterminate ${\mathbf {A}_{n}^{2}}$
-complexes. Note that wedge summands of the form $\bigvee _{i=u}^vX$
with $v< u$
are contractible and can be removed from the homotopy decompositions of $\Sigma M$
. More generally, if $M$
is a $5$
-dimensional Poincaré duality complex (i.e., a finite CW-complex whose integral cohomology satisfies the Poincaré duality theorem) satisfying the conditions in Theorem 1.1, then Theorem 1.1 gives the homotopy types of $\Sigma M$
, except that there are two additional possibilities when the Steenrod square acts trivially on $H^3(M; {\mathbb {Z}/2^{}})$
, See remark 4.5.
Due to lemma 2.3 (2), the $3$
-torsion of $H$
can be well understood when studying the homotopy types of the double suspension $\Sigma ^2 M$
.
Theorem 1.2 Let $M$
be an orientable smooth closed $five$
-manifold with $H_\ast (M)$
given by (1.1), where $H$
is a $2$
-torsion free group. Then the suspensions of the homotopy equivalences in Theorem 1.1 give the homotopy types of the double suspension $\Sigma ^2M$
.
In addition to the characterization of the homotopy types of iterated loop spaces of the gauge groups of principal bundles over $M$
, as shown by Huang [Reference Huang9], we apply the homotopy types of $\Sigma M$
(or $\Sigma ^2M$
) to study the reduced $K$
-groups and the cohomotopy sets $\pi ^k(M)=[M,\,S^k]$
of the non-simply-connected manifold $M$
.
Corollary 1.3 (See proposition 5.2)
Let $M$
be a five-manifold given by Theorems 1.1 or 1.2. Then the reduced complex $K$
-group and $KO$
-group of $M$
are given by
The third cohomotopy set $\pi ^3(M)$
possess the following property.
Corollary 1.4 (See proposition 5.6)
Let $M$
be a five-manifold given by Theorems 1.1 or 1.2. Then the suspension $\Sigma \colon \pi ^3(M)\to \pi ^4(\Sigma M)$
is a bijection.
We also apply the homotopy decompositions of $\Sigma M$
to compute the group structure of $\pi ^3(M)\cong \pi ^4(\Sigma M)$
, see proposition 5.6. The second cohomotopy set $\pi ^2(M)$
always admits an action of $\pi ^3(M)$
induced by the Hopf map $\eta \colon S^3\to S^2$
, see lemma 5.3 or [Reference Kirby, Melvin and Teichner13, Theorem 3]. Finally, it should be noting that when $M$
is a $5$
-dimensional Poincaré duality complex with $H_1(M)$
torsion free, similar results have been proved independently and concurrently by Amelotte, Cutler and So [Reference Amelotte, Cutler and So1].
This paper is organized as follows. Section 2 reviews some homotopy theory of ${\mathbf {A}_{n}^{2}}$
-complexes and introduces the basic analysis methods to study the homotopy type of homotopy cofibres. In § 3 we study the homotopy types of the suspension of the CW-complex $\overline {M}$
of $M$
with its top cell removed. The basic method is the homology decomposition of simply-connected spaces. Section 4 analyzes the homotopy types of $\Sigma M$
and contains the proofs of Theorems 1.1 and 1.2. As applications of the homotopy decomposition of $\Sigma M$
or $\Sigma ^2M$
, we study the reduced $K$
-groups and the cohomotopy sets of the five-manifolds $M$
in § 5.
2. Preliminaries
Throughout the paper we shall use the following global conventions and notations. All spaces are based CW-complexes, all maps are base-point-preserving and are identified with their homotopy classes in notation. A strict equality is often treated as a homotopy equality. Denote by $\unicode{x1D7D9}_X$
the identity map of a space $X$
and simplify $\unicode{x1D7D9}_n=\unicode{x1D7D9}_{S^n}$
. For different $X$
, we use the ambiguous notations $i_k\colon S^k\to X$
and $q_k\colon X\to S^k$
to denote the possible canonical inclusion and pinch maps, respectively. For instance, there are inclusions $i_n\colon S^n\to C$
for each elementary Chang complex $C$
and there are inclusions $i_{n+1}\colon S^{n+1}\to X$
for $X=C^{n+2,s}$
and $C^{n+2,s}_r$
. Let $i_P\colon P^{n+1}(2^r)\to C^{n+2}_r$
and $i_\eta \colon C^{n+2}_\eta \to C^{n+2}_r$
be the canonical inclusions. Denote by $C_f$
the homotopy cofibre of a map $f\colon X\to Y$
. For an abelian group $G$
generated by $x_1,\,\cdots,\,x_n$
, denote $G\cong C_1\langle x_1\rangle \oplus \cdots \oplus C_n\langle x_n\rangle$
if $x_i$
is a generator of the cyclic direct summand $C_i$
, $i=1,\,\cdots,\,n$
.
2.1 Some homotopy theory of $\mathbf {A}_n^2$-complexes
For each prime $p$
and integers $r,\,s\geq 1,\,n\geq 2$
, there exists a map (with $n$
omitted in notation)
satisfies $\Sigma B(\chi ^r_s)=B(\chi ^r_s)$
and the relation formulas (cf. [Reference Baues and Hennes3]):
where $\chi ^r_s$
is a self-map of spheres, $\chi ^r_s=1$
for $r\geq s$
and $\chi ^r_s=p^{s-r}$
for $r< s$
.
Lemma 2.1 Let $p$
be an odd prime and let $n\geq 3$
, $r,\,s\geq 1$
be integers, $m=\min \{r,\,s\}$
. There hold isomorphisms:
(1) $\pi _3(P^3(p^r))\cong {\mathbb {Z}/p^{r}}\langle i_2\eta \rangle$
and $\pi _{n+1}(P^{n+i}(p^r))=0$, $i=0,\,1$.(2) $[P^n(p^r),\,P^n(p^s)]\cong \left \{\begin{array}{@{}ll} {\mathbb {Z}/p^{m}}\langle B(\chi ^r_s)\rangle \oplus {\mathbb {Z}/p^{m}}\langle i_2\eta q_3\rangle,\, & n=3;\\ {\mathbb {Z}/p^{m}}\langle B(\chi ^r_s)\rangle,\, & n\geq 4. \end{array}\right.$
(3) $[P^{n+1}(p^r),\,P^n(p^s)]\cong \left \{\begin{array}{@{}ll} {\mathbb {Z}/p^{m}}\langle \hat {\eta }_s B(\chi ^r_s)\rangle,\, & n\!=\!3;\\ 0 & n\!\geq\! 4. \end{array}\right.$
where $\hat {\eta }_s\colon P^4(p^s)\to P^3(p^s)$ satisfies $\hat {\eta }_si_3=i_2\eta$.
Proof. The group $\pi _3(P^3(p^r))$
refers to [Reference So and Theriault21, Lemma 2.1] and the groups $\pi _{n+1}(P^{n+i})=0$
was proved in [Reference Huang11, Lemma 6.3 and 6.4]. The groups and generators in (2) and (3) can be easily computed by applying the exact functor $[-,\,P^n(p^s)]$
to the canonical cofibrations for $P^{n+i}(p^r)$
with $i=0,\,1$
, respectively; the details are omitted here.
Lemma 2.2 (cf. [Reference Baues and Hennes3])
Let $n\geq 3,\,r\geq 1$
be integers.
(1) $\pi _{n+1}(P^{n+1}(2^r))\cong {\mathbb {Z}/2^{}}\langle i_n\eta \rangle$
.(2) $\pi _{n+2}(P^{n+1}(2^r))\cong \left \{\begin{array}{@{}ll} {\mathbb {Z}}/4\langle \tilde {\eta }_1\rangle,\, & r=1;\\ {\mathbb {Z}}/2\oplus {\mathbb {Z}/2^{}}\langle \tilde {\eta }_r,\,i_n\eta ^2\rangle,\, & r\geq 2. \end{array}\right.$
The generator $\tilde {\eta }_r$
satisfies formulas
(2.2)\begin{equation} q_{n+1}\tilde{\eta}_r=\eta,\quad 2\tilde{\eta}_1=i_n\eta^2,\quad B(\chi^r_s)\tilde{\eta}_r=\chi^s_r\cdot\tilde{\eta}_s. \end{equation}
(3) $[P^{n+1}(2^r),\,P^{n+1}(2^s)]\cong \left \{\begin{array}{@{}ll} {\mathbb {Z}}/4\langle \unicode{x1D7D9}_P\rangle,\, & r=s=1;\\ {\mathbb {Z}/2^{m}}\langle B(\chi ^r_s)\rangle \oplus {\mathbb {Z}/2^{}}\langle i\eta q\rangle,\, & \textrm {otherwise},\, \end{array}\right.$
where $m=\min \{r,\,s\}$
, $i\eta q=i_n\eta q_{n+1}$.
Lemma 2.3 The following hold:
(1) $\pi _5(P^3(3^r))\cong {\mathbb {Z}}/3^{r+1}$
, $\pi _5(P^3(p^r))=0$ for primes $p\geq 5$.(2) The suspension $\Sigma \colon \pi _5(P^3(3^r))\to \pi _6(P^4(3^r))$
is trivial.
Proof. (1) Let $F^3\{p^r\}$
be the homotopy fibre of $q_3\colon P^3(p^r)\to S^3$
and consider the induced exact sequence of $p$
-local groups:
By [Reference Neisendorfer18, Proposition 14.2] or [Reference Neisendorfer19, Theorem 3.1], there is a homotopy equivalence
where $S^{2n+1}\{p^r\}$
is the homotopy fibre of the mod $p^r$
degree map on $S^{2n+1}$
, $n_\alpha \geq 4$
and the equality holds for exactly one $\alpha$
. It follows that
Thus $\pi _5(P^3(p^r))=0$
for $p\geq 5$
. By [Reference Neisendorfer19, Theorem 2.10], $\pi _5(P^3(3^r))$
contains a direct summand ${\mathbb {Z}}/3^{r+1}$
, therefore we have an isomorphism
(2) Firstly, by [Reference Cohen, Moore and Neisendorfer6] for any prime $p\geq 5$
and [Reference Neisendorfer19] for $p=3$, there is a homotopy equivalence
Second, for skeletal reasons, the suspension $E\colon P^3(p^r)\to \Omega P^4(p^r)$
factors as the composite $P^3(p^r)\mathop\longrightarrow\limits^ {i}S^3\{p^r\}\mathop\longrightarrow\limits^ {j}\Omega P^4(p^r)$
, where $i$
is the inclusion of the bottom Moore space and $j$
is the inclusion of a factor. Third, there is a homotopy fibration diagram
that defines the space $E^3\{p^r\}$
. By [Reference Cohen, Moore and Neisendorfer5], for any prime $p\geq 5$
and [Reference Neisendorfer19] for $p=3$
, there is a homotopy equivalence
where $W_n$
is the homotopy fibre of the double suspension. This decomposition has the property that the factor $\prod _{j=1}^{\infty }S^{2p^j-1}\{p^{r+1}\}$
of $\Omega F^3\{p^r\}$
may be chosen to factor through $\Omega E^3\{p^r\}$
.
Consequently, when $p=3$
, as the ${\mathbb {Z}}/3^{r+1}$
factor in $\pi _4(\Omega P^3(p^r))$
came from $\pi _4(\prod _{j=1}^{\infty }S^{2p^j-1}\{p^{r+1}\})$
, it has the property that it composes trivially with the map $\Omega i\colon \Omega P^3(3^r)\to \Omega S^3\{3^r\}$
. Hence, as $\Omega E$
factors through $\Omega i$
, the ${\mathbb {Z}}/3^{r+1}$
factor in $\pi _4(\Omega P^3(p^r))$
composes trivially with $\Omega E$
. Thus the ${\mathbb {Z}}/3^{r+1}$
factor in $\pi _5(P^3(p^r))$
suspends trivially.
Lemma 2.4 (cf. [Reference Li14])
Let $n\geq 3$
and $r\geq 1$
. There hold isomorphisms
(1) $\pi _{n+2}(C^{n+2}_\eta )\cong {\mathbb {Z}}\langle \tilde {\zeta }\rangle$
, where $\tilde {\zeta }$ satisfies $q_{n+2}\tilde {\zeta }=2\cdot \unicode{x1D7D9}_{n+2}$.(2) $\pi _{n+2}(C^{n+2}_r)\cong {\mathbb {Z}}\langle i_\eta \tilde {\zeta }\rangle \oplus {\mathbb {Z}/2^{}}\langle i_P\tilde {\eta }_r\rangle$
.
It follows that a map $f_C\colon S^{n+2}\to C$
with $C=C^{n+2}_\eta$
or $C^{n+2}_r$
induces the trivial homomorphism in integral homology if and only if
where $f=0$
means $f$
is null-homotopic.
The following Lemma can be found in [Reference Li14, Theorem 3.1, (2)]; since it hasn't been published yet, we give a proof here.
Lemma 2.5 For integers $n\geq 3$
and $r\geq 1$
, there exists a map
satisfying the homotopy commutative diagram of homotopy cofibrations
Moreover, there hold formulas
Proof. Dual to the relation in lemma 2.4 (1), there exists a map $\bar {\zeta }\colon C^{n+2}_\eta \to S^n$
satisfying $\bar {\zeta }i_n=2\cdot \unicode{x1D7D9}_n$
. It follows that the first square in the Lemma is homotopy commutative, and hence the map $\bar {\xi }_r$
in the Lemma exists. Recall we have the composition
Then $\bar {\xi }_ri_n=(\bar {\xi }_ri_\eta ) i_n=(i_n\bar {\zeta })i_n=2i_n$
implying that
for some $\varepsilon \in \{0,\,1\}.$
If $\varepsilon =0$
, we are done; otherwise we replace $\bar {\xi }_r$
by $\bar {\xi }_r+i_n\eta q_{n+1}$
to make $\varepsilon =0$
. Note that all the relations mentioned above still hold even if we make such a replacement. Thus we prove the first formula in (2.3), which implies the second one.
2.2 Basic analysis methods
We give some auxiliary lemmas that are useful to study the homotopy types of homotopy cofibres.
Lemma 2.6 Let $C_k^X$
be the homotopy cofibre of $f^X_k\colon X\to P^3(p^s)$
, where $k\in {\mathbb {Z}/p^{\min \{r,\,s\}}}$
and $r=\infty$
for $X=S^3$
,
Then the cup squares in $H^\ast (C_k^X; {\mathbb {Z}/p^{\min \{r,\,s\}}})$
are given by
where $u_i\in H^i(C_k^X; {\mathbb {Z}/p^{\min \{r,\,s\}}})$
are generators, $i=2,\,4$
. It follows that all cup squares in $H^\ast (C_k^X; {\mathbb {Z}/p^{\min \{r,\,s\}}})$
are trivial if and only if $k=0$
.
Proof. It is well-known that the map $k\eta$
has Hopf invariant $H(k\eta )=kH(\eta )=k$
. Let $m=\min \{r,\,s\}$
and define $u_2\smallsmile u_2=\bar {H}(f_k^X)\cdot u_4$
for some $\bar {H}(f_k^X)\in {\mathbb {Z}/p^{m}}$
, which is called the mod $p^m$
Hopf invariant. Then by naturality it is easy to deduce the formula
which completes the proof of the Lemma.
Lemma 2.7 Let $k\in {\mathbb {Z}/p^{\min \{r,\,s\}}}$
and consider the homotopy cofibration
Let $v_i$
be generators of $H^i(C_{g_k}; {\mathbb {Z}/p^{s}})$
, $i=2,\,4$
, then
It follows that $g_k$
is null-homotopic if and only if $k=0$
.
Proof. By lemma 2.1 (3), there is a homotopy commutative diagram of homotopy cofibrations
It follows that $\imath$
in the right-most column induces an isomorphism
and a monomorphism
Let $v_i\in H^i(C_{g_k}; {\mathbb {Z}/p^{s}})$
be generators, $i=2,\,4$
; let $u_2=\imath ^\ast (v_2)$
and $u_4$
be generators of $H^2(C_{k\chi ^r_s}; {\mathbb {Z}/p^{s}})$
and $H^4(C_{k\chi ^r_s}; {\mathbb {Z}/p^{s}})$
, respectively. Let $\bar {H}(g_k)$
be the mod $p^s$
Hopf invariant of $g_k$
. By the naturality of cup products and lemma 2.6, we have
Thus $\bar {H}(g_k)=k$
, which completes the proof.
The method of proof for the following lemma is due to [Reference Cutler and So7, Lemma 2.4].
Lemma 2.8 Let $X_1,\,X_2\in \{S^2,\,P^3(2^r),\,C^4_s\}$
with $r,\,s\geq 1$
. Let
be the canonical inclusion maps. Then any map $u'$
in the composition
is null-homotopic if and only if all cup products in $H^\ast (C_u;G)$
are trivial, where $C_u$
is the homotopy cofibre of $u$
and $G=H_2(X_1)\otimes H_2(X_2)$
.
Proof. The ‘only if’ part is clear. For the ‘if’ part, consider the following homotopy commutative diagram of homotopy cofibrations
which induces the commutative diagram with exact rows and columns:
Note that $H^6(\Sigma X_1\times \Sigma X_2;G)$
is generated by cup products, while all cup products in $H^6(C_u;G)$
are trivial by assumption. It follows that $\bar {j}^\ast =0$
and hence $\delta _1$
is surjective. The homomorphism $\delta _2$
is obviously an isomorphism for $X_1,\,X_2\in \{S^2,\,P^3(2^r)\}$
because $H^5(\Sigma X_1\vee \Sigma X_2;G)=0$
; for $X_2=C^4_s$
, $X_1=S^2,\,P^3(2^r)$
or $C^4_r$
, we have $H^j(C^4_s;G)\cong G$
for $j=2,\,3,\,4$
, where $G= {\mathbb {Z}/2^{s}}$
or ${\mathbb {Z}/2^{\min \{r,\,s\}}}$
. By computations,
Thus $\delta _2$
is an isomorphism for all $X_1,\,X_2$
. The upper commutative square then implies that $(i')^\ast$
is surjective and therefore $(u')^\ast$
is the zero map by exactness. Since $\Sigma X_1\wedge X_2$
is $4$
-connected, the universal coefficient theorem for cohomology implies that
Therefore $u'$
is null-homotopic, by the Hurewicz theorem.
Lemma 2.9 The Steenrod square $\operatorname {Sq}^2\colon H^{n}(C; {\mathbb {Z}/2^{}})\to H^{n+2}(C; {\mathbb {Z}/2^{}})$
is an isomorphism for every $(n+2)$
-dimensional elementary Chang complex $C$
.
Proof. Obvious or see [Reference Zhu and Pan27].
For $n\geq 3$
and $r\geq 1$
, we define homotopy cofibres
Lemma 2.10 The Steenrod square $\operatorname {Sq}^2\colon H^{n+1}(X; {\mathbb {Z}/2^{}})\to H^{n+3}(X; {\mathbb {Z}/2^{}})$
is an isomorphism for $X= A^{n+3}(\tilde {\eta }_r)$
and $A^{n+3}(i_P\tilde {\eta }_r)$
.
Proof. The statement for $X= A^{n+3}(\tilde {\eta }_r)$
refers to [Reference Li15, Lemma 2.6]. For $X=A^{n+3}(i_P\tilde {\eta }_r)$
, consider the homotopy commutative diagram of homotopy cofibrations
From the first two rows of the homotopy commutative diagram, it is easy to compute that
The third column homotopy cofibration implies that the induced homomorphisms $\imath ^\ast$
are monomorphisms of mod $2$
homology groups of dimension $n+1$
and $n+3$
, hence it is an isomorphism. Then we complete the proof by the naturality of $\operatorname {Sq}^2$
.
Lemma 2.11 (Lemma 6.4 of [Reference Huang and Li12])
Let $S\mathop\longrightarrow\limits^ {f}\left (\bigvee _{i=1}^nA_i\right )\vee B \mathop\longrightarrow\limits^ {g}\Sigma C$
be a homotopy cofibration of simply-connected CW-complexes. For each $j=1,\,\cdots,\, n$
, let
be the obvious projections. Suppose that the composite $p_jf$
is null-homotopic for each $j\leq n$
, then there is a homotopy equivalence
where $C_{q_Bf}$
is the homotopy cofibre of the composite $q_Bf$
.
Lemma 2.12 Let $\left (\bigvee _{i=1}^nA_i\right )\vee B \mathop\longrightarrow\limits^ {f}C\to D$
be a homotopy cofibration of CW-complexes. If the restriction of $f$
to $A_i$
is null-homotopic for each $i=1,\,\cdots,\,n$
, then there is a homotopy equivalence
where $E$
is the homotopy cofibre of the restriction $f|B\colon B\to C$
.
Proof. Clear.
Let $X=\Sigma X'$
, $Y_i=\Sigma Y_i'$
be suspensions, $i=1,\,2,\,\cdots,\,n$
. Let
be respectively the canonical inclusions and projections, $1\leq k,\,l\leq n$
. By the Hilton–Milnor theorem, we may write a map $f\colon X\to \bigvee _{i=1}^nY_i$
as
where $f_{k}=p_k\circ f\colon X\to Y_k$
and $\theta$
satisfies $\Sigma \theta =0$
. The first part $\sum _{k=1}^n i_k\circ f_{k}$
is usually represented by a vector $u_f=(f_1,\,f_2,\,\cdots,\,f_n)^t.$
We say that $f$
is completely determined by its components $f_k$
if $\theta =0$
; in this case, denote $f=u_f$
. Let $h=\sum _{k,l}i_lh_{lk}p_k$
be a self-map of $\bigvee _{i=1}^nY_i$
which is completely determined by its components $h_{kl}=p_k\circ h\circ i_l\colon Y_l\to Y_k$
. Denote by
Then the composition law $h(f+g)\simeq h f+h g$
implies that the product
given by the matrix multiplication represents the composite $h\circ f$
. Two maps $f=u_f$
and $g=u_g$
are called equivalent, denoted by
if there is a self-homotopy equivalence $h$
of $\bigvee _{i=1}^n Y_i$
, which can be represented by the matrix $M_h$
, such that
Note that the above matrix multiplication refers to elementary row operations in matrix theory; and the homotopy cofibres of the maps $f=u_f$
and $g=u_g$
are homotopy equivalent if $f$
and $g$
are equivalent.
3. Homology decomposition of $\Sigma M$
Recall the homology decomposition of a simply-connected space $X$
(cf. [Reference Hatcher8, Theorem 4H.3]). For $n\geq 2$
, the $n$
th homology section $X_n$
of $X$
is a CW-complex constructed from $X_{n-1}$
by attaching a cone on a Moore space $M(H_nX,\,n-1)$
; by definition, $X_1=\ast$
. Note that for each $n\geq 2$
, there is a canonical map $j_n\colon X_n\to X$
that induces an isomorphism $j_{n\ast }\colon H_r(X_n)\to H_r(X)$
for $r\leq n$
and $H_r(X_n)=0$
for $r>n$
.
Firstly we note that similar arguments to the proof of [Reference So and Theriault21, Lemma 5.1] proves the following lemma.
Lemma 3.1 Let $M$
be an orientable closed manifold with $H_1(M)\cong {\mathbb {Z}}^l\oplus H$
, where $l\geq 1$
and $H$
is a torsion abelian group. Then there is a homotopy equivalence
where $W=M/\bigvee _{i=1}^l S^1$
is the quotient space with $H_1(W)\cong H$
.
By lemma
3.1 and (1.1), the homology groups of $\Sigma W$
is given by
Let $W_i$
be the $i$
th homology section of $\Sigma W$
. There are homotopy cofibrations in which the attaching maps are homologically trivial (induce trivial homomorphisms in integral homology):
From now on we assume that $H\cong \bigoplus _{j=1}^h {\mathbb {Z}}/q_j^{s_j}$
where $q_j$
are odd primes and $s_j\geq 1$
.
Lemma 3.2 There is a homotopy equivalence
Proof. It suffices to show the map $f$
in (3.2) is null-homotopic, or equivalently the following components of $f$
are null-homotopic:
where $\hookrightarrow$
denote the canonical inclusion maps. $f$
is homologically trivial, so are $f^{S}$
and $f^{T}$
. Then the Hurewicz theorem and lemma 2.1 (1) imply $f^{S}$
is null-homotopic.
Since $[P^3(p^r),\,P^3(q^s)]=0$
for different primes $p,\,q$
, it suffices to consider the case where $T$
and $H$
have the same prime factors. Denote by $T_H\cong \bigoplus _{j} {\mathbb {Z}}/q_j^{r_j}$
the component of $T$
that has the same prime factors with $H$
. The canonical inclusion $\imath _3\colon W_3\to \Sigma W$
induces an isomorphism with $m_j=\min \{r_j,\,s_j\}$
:
It follows that all the cup squares of cohomology classes of $H^2(W_3; {\mathbb {Z}}/q_j^{m_j})$
, and hence of $H^2(C_{f^T}; {\mathbb {Z}}/q_j^{m_j})$
are trivial for any $j$
. Let $C_{f^T_j}$
be the homotopy cofibre of the compositions
where the unlabelled maps are the canonical inclusions and projections, respectively. Then [Reference So and Theriault21, Lemma 4.2] implies that all cup squares of cohomology classes of $H^2(C_{f^T_j}; {\mathbb {Z}}/q_j^{m_j})$
are trivial for any $j$
and hence $f^T_j$
is null-homotopic, by lemma 2.6. Therefore $f^T$
is also null-homotopic and we complete the proof.
Lemma 3.3 There is a homotopy equivalence
Proof. By (3.2) and lemma 3.2, $W_4$
is the homotopy cofibre of a homologically trivial map
Consider the compositions
where the unlabelled maps are the canonical inclusions and projections. Since $[P^4(p^r),\,S^3]=0$
, the Hurewicz theorem and lemma 2.1 (2) imply that all the above compositions are null-homotopic. Hence by lemma 2.11 there is a homotopy equivalence
for some map $g'\colon \left (\bigvee _{i=1}^dS^3\right )\vee P^4(H)\to P^3(H)$
.
By the homology decomposition for $\Sigma W$
and the universal coefficient theorem for cohomology, the canonical map $\imath _4\colon W_4\to \Sigma W$
induces isomorphisms
Consider the commutative diagram
where $\smallsmile ^2$
denotes the cup squares. All cup squares in $H^\ast (\Sigma W; {\mathbb {Z}}/q_j^{s_j})$
are trivial implying that all cup squares in $H^4(W_4; {\mathbb {Z}}/q_j^{s_j})$
are trivial. Let $C_{g'_j}$
and $C_{g'_{ij}}$
be the homotopy cofibres of the compositions
By [Reference So and Theriault21, Lemma 4.2], we get the triviality of cup squares in $H^\ast (C_{g'_j}; {\mathbb {Z}}/q_j^{s_j})$
and $H^\ast (C_{g'_{ij}}; {\mathbb {Z}}/q_j^{s_j}))$
. Then lemmas 2.6 and 2.7 imply that $g_j'$
and $g'_{ij}$
are both null-homotopic. Thus by lemma 2.12, there is a homotopy equivalence
which completes the proof of the Lemma.
Proposition 3.4 There is a homotopy equivalence
where $0\leq c_1 \leq \min \{l,\,d\}$
and $0\leq c_2\leq \min \{l-c_1,\,t_2\}$
; $c_1=c_2=0$
if and only if $\operatorname {Sq}^2(H^2(M; {\mathbb {Z}/2^{}}))=0$
.
Proof. By (3.2) and lemma 3.3, $W_5$
is the homotopy cofibre of a map
Similar arguments to that in the proof of lemma 3.3 show that there is a homotopy equivalence
where $h'\colon \bigvee _{i=1}^lS^4\to \left (\bigvee _{i=1}^dS^3\right )\vee \left (\bigvee _{i=1}^{t_2}P^4(2^{r_i})\right )$
.
Since $\pi _4(P^4(2^r))\cong {\mathbb {Z}/2^{}}\langle i_3\eta \rangle$
, we may represent the map $h'$
by a $(d+t_2)\times l$
-matrix $M_{h'}$
with entries $0$
, $\eta$
or $i_3\eta$
. There hold homotopy equivalences
Then by elementary matrix operations we have an equivalence
where $O$
denote suitable zero matrices, $D_{c_1}$
is the diagonal matrix of rank $c_1$
whose diagonal entries are $\eta$
, $E_{c_2}$
is a $c_2\times c_2$
-matrix which has exactly one entry $i_3\eta$
in each row and column. It follows that there is a homotopy equivalence
4. Proof of Theorems 1.1 and 1.2
Let $M$
be the given five-manifold described in Theorem 1.1. By (3.2) there is a homotopy cofibration $S^5\mathop\longrightarrow\limits^ {\phi }W_5\to \Sigma W$
with $W_5$
(and integers $c_1,\,c_2$
) given by proposition 3.4. Since $\phi$
is homologically trivial, so are the compositions
By lemma 2.4, $\phi _\eta$
is null-homotopic and $\phi _{C_j}=w_j\cdot i_P\tilde {\eta }_{r_j}$
for some $w_j\in {\mathbb {Z}/2^{}}$
. By lemma 2.3, $\phi _{H,j}$
is null-homotopic for primes $q_j\geq 5$
and $\Sigma \phi _{H,j}$
are null-homotopic for all odd primes $q_j$
. Write $H=H_3\oplus H_{\geq 5}$
with $H_3$
the $3$
-primary component of $H$
. It follows by lemmas 2.1 (2) and 2.11 that there are homotopy equivalences
for some homologically trivial map
From now on we assume that $H_3=0$
to study the homotopy type of $\Sigma W$
or the homotopy cofibre $C_{\bar {\phi }}$
. By lemmas 2.2 and 2.4 we may put
where all coefficients belong to ${\mathbb {Z}/2^{}}$
and $\theta$
is a linear combination of Whitehead products. By the Hilton-Milnor theorem the domain $\operatorname {Wh}$
of $\theta$
is given by
Note that all the spaces $\Sigma X_i\wedge X_j$
are $4$
-connected and hence there are Hurewicz isomorphisms $\pi _5(\Sigma X_i\wedge X_j)\cong H_5(\Sigma X_i\wedge X_j)$
. For different $X_i$
and $X_j$
, we use the ambiguous notations
to denote the natural inclusions. Then we can write
where
Since the homotopy cofibre of $\phi$
is $\Sigma W$
, similar arguments to the proof of [Reference Cutler and So7, Lemma 4.2] show the following lemma.
Lemma 4.1 Let $C_u$
be the homotopy cofibre of a map $u$
with $u$
given by (1) $u=a_{ij}$
, (2) $u=b_{ij}$
, (3) $u=c_{ij}$
, (4) $u=d_{ij}$
, (5) $u=e_{ij}$
, (6) $u=f_{ij}$
. Then all cup products in $H^\ast (C_u;R)$
are trivial for any principal ideal domain $R$
.
By lemmas 4.1 and 2.8 we then get
Corollary 4.2 The Whitehead product component $\theta$
(4.4) of $\bar {\phi }$
is trivial.
For each $n\geq 2$
, let $\Theta _n$
be secondary cohomology operation based on the null-homotopy of the composition
where $K_m=K( {\mathbb {Z}/2^{}},\,m)$
denotes the Eilenberg–MacLane space of type $( {\mathbb {Z}/2^{}},\,m)$
. More concretely, $\Theta _n\colon S_n(X)\to T_n(X)$
is a cohomology operation with
Note that $\Theta _n$
detects the maps $\eta ^2\in \pi _{n+2}(S^n)$
and $i_n\eta ^2\in \pi _{n+2}(P^{n+1}(2^r))$
(cf. [Reference Li15, Section 2.4]). By the method outlined in [Reference Madsen and Milgram16, page 32], the stable secondary operation $\Theta =\{\Theta _n\}_{n\geq 2}$
is spin trivial (cf. [Reference Thomas24]), which means the following Lemma holds.
Lemma 4.3 The secondary operation $\Theta \colon H^\ast (M; {\mathbb {Z}/2^{}})\to H^{\ast +3}(M; {\mathbb {Z}/2^{}})$
is trivial for any orientable closed smooth spin manifold $M$
.
Now we are prepared to classify the homotopy types of $C_{\bar {\phi }}$
. Note that for a closed orientable smooth five-manifold $M$
, the second Stiefel–Whitney class equals the second Wu class $v_2$
, which satisfies $\operatorname {Sq}^2(x)=v_2\smallsmile x$
for all $x\in H^3(M; {\mathbb {Z}/2^{}})$
[Reference Milnor and Stasheff17, page 132]. It follows that the orientable smooth five-manifold $M$
is spin if and only if $\operatorname {Sq}^2$
acts trivially on $H^3(M; {\mathbb {Z}/2^{}})$
, which is equivalent to $\operatorname {Sq}^2$
acting trivially on $H^4(\Sigma W; {\mathbb {Z}/2^{}})$
or $H^4(C_{\bar {\phi }}; {\mathbb {Z}/2^{}})$
, by lemma 3.1 and the homotopy decomposition (4.1).
Proposition 4.4 If $M$
is a closed orientable smooth spin five-manifold, then there is a homotopy equivalence
Proof. The smooth spin condition on $M$
, together with lemma 4.3, implies that $x_i=\epsilon _j=0$
for all $i,\,j$
in (4.3). By the comments above proposition 4.4, $M$
is spin implies that the Steenrod square $\operatorname {Sq}^2$
acts trivially on $H^4(C_{\bar {\phi }}; {\mathbb {Z}/2^{}})$
. Then lemmas 2.9 and 2.10 imply $y_i=z_j=w_j=0$
for all $i,\,j$
. Thus the map $\bar {\phi }$
in (4.3) is null-homotopic and therefore we get the homotopy equivalence in the Proposition.
Remark 4.5 If $M$
is a general $5$
-dimensional connected Poincaré duality complex such that $\operatorname {Sq}^2$
acts trivially on $H^3(M; {\mathbb {Z}/2^{}})$
, then we have the following two additional possibilities for the homotopy types of $C_{\bar {\phi }}$
in terms of the secondary cohomology operation $\Theta$
:
(1) If for any $u\in H^3(M; {\mathbb {Z}/2^{}})$
with $\Theta (u)\neq 0$ and any $v\in \ker (\Theta )$, there holds $\beta _r(u+v)=0$ for all $r$, then there is a homotopy equivalence
\[ C_{\bar{\phi}}\simeq \left(\bigvee_{i=2}^{d-c_1}S^3\right)\vee \left(\bigvee_{i=1}^{d}S^4\right)\vee \left(\bigvee_{j=c_2+1}^{t_2}P^4(2^{r_j})\right)\!\vee\! \left(\bigvee_{j=1}^{c_2}C^5_{r_j}\right)\!\vee\! (S^3\cup_{\eta^2}\,{\rm e}^6). \]
(2) If there exist $u\in H^3(M; {\mathbb {Z}/2^{}})$
with $\Theta (u)\neq 0$ and $v\in \ker (\Theta )$ such that $\beta _r(u+v)\neq 0$, then there is a homotopy equivalence
\[ C_{\bar{\phi}}\simeq \left(\bigvee_{i=1}^{d-c_1}S^3\right)\!\vee\! \left(\bigvee_{i=1}^{d}S^4\right)\!\vee\! \left(\bigvee_{j_0\!\neq\! j=c_2+1}^{t_2}P^4(2^{r_j})\right)\!\vee\! \left(\bigvee_{j=1}^{c_2}C^5_{r_j}\right)\!\vee\! A^6(2^{r_{j_0}}\eta^2), \]where $A^6(2^{r_{j_0}}\eta ^2)=P^4(2^{r_{j_0}})\cup _{i_3\eta ^2}\,{\rm e}^6$
, $j_0$ is the index such that $r_{j_0}$ is the maximum of $r_j$ satisfying $\beta _{r_j}(u+v)\neq 0$.
Proposition 4.6 Suppose that $\operatorname {Sq}^2$
acts non-trivially on $H^3(M; {\mathbb {Z}/2^{}})$
, or equivalently $\operatorname {Sq}^2$
acts non-trivially on $H^4(C_{\bar {\phi }}; {\mathbb {Z}/2^{}})$
.
(1) If for any $u,\, v\in H^4(C_{\bar {\phi }}; {\mathbb {Z}/2^{}})$
satisfying $\operatorname {Sq}^2(u)\neq 0$ and $\operatorname {Sq}^2(v)=0$, there holds $u+v\notin \operatorname {im}(\beta _r)$ for any $r\geq 1$, then there is a homotopy equivalence
\[ C_{\bar{\phi}}\simeq \left(\bigvee_{i=1}^{d-c_1}S^3\right)\vee \left(\bigvee_{i=2}^{d}S^4\right)\vee \left(\bigvee_{j=c_2+1}^{t_2}P^4(2^{r_j})\right)\vee\left(\bigvee_{j=1}^{c_2}C^5_{r_j}\right)\vee C^6_\eta. \]
(2) If there exist $u,\, v\in H^4(C_{\bar {\phi }}; {\mathbb {Z}/2^{}})$
with $\operatorname {Sq}^2(u)\neq 0$ and $v\in \ker (\operatorname {Sq}^2)$ such that $u+v\in \operatorname {im}(\beta _r)$ for some $r$, then either there is a homotopy equivalence
\[ C_{\bar{\phi}}\simeq \left(\bigvee_{i=1}^{d-c_1}S^3\right)\!\vee\! \left(\bigvee_{i=1}^{d}S^4\right)\!\vee\! \left(\bigvee_{j_1\!\neq\! j=c_2+1}^{t_2}P^4(2^{r_j})\right)\!\vee\!\left(\bigvee_{j=1}^{c_2}C^5_{r_j}\right)\!\vee\! A^6(\tilde{\eta}_{r_{j_1}}), \]or there is a homotopy equivalence
\[ C_{\bar{\phi}}\simeq \left(\bigvee_{i=1}^{d-c_1}S^3\right)\!\vee\! \left(\bigvee_{i=1}^{d}S^4\right)\!\vee\! \left(\bigvee_{j=c_2+1}^{t_2}P^4(2^{r_j})\right)\!\vee\!\left(\bigvee_{j_1\neq j=1}^{c_2}C^5_{r_j}\right)\!\vee\! A^6(i_P\tilde{\eta}_{r_{j_1}}), \]where the last two complexes are defined by (2.4) and $r_{j_1}$
is the minimum of $r_j$ such that $u+v\in \operatorname {im}(\beta _{r_j})$.
Proof. Recall the equation for $\bar {\phi }$
given by (4.3). Since $\operatorname {Sq}^2$
acts non-trivially on $H^4(C_{\bar {\phi }}; {\mathbb {Z}/2^{}})$
, at least one of $y_i,\,z_j,\,w_j$
equals $1$
.
(1) The conditions in (1) implying that $z_j=w_j=0$
for all $j$ and hence $y_i=1$ for some $i$. Clearly we may assume that $y_1=1$ and $y_i=0$ for all $2\leq i\leq d$. By the equivalences
we may further assume that $x_i=\epsilon _i=0$
for all $i$
in (4.3). Thus we have
which proves the homotopy equivalence in (1).
(2) The conditions in (2) implies that $z_j=1$
or $w_j=1$ for some $j$. For maps $\tilde {\eta }_r,\,i_3\eta ^2\colon S^5\to P^4(2^r)$ and $i_P\tilde {\eta }_s\colon S^5\to C^5_s$, the formulas (2.1) and (2.2) indicate the following equivalences
It follows that we may assume that $x_i=y_i=0$
for all $i$
regardless of whether $z_j=1$
or $w_j=1$
.
(i) If $z_j=1$
for some $j$, we assume that $z_j=1$ for exactly one $j$, say $z_{j_1}=1$; in this case, $\epsilon _j=0$ for all $j\neq j_1$. Note that $\unicode{x1D7D9}_P+i_3\eta q_4$ is a self-homotopy equivalence of $P^4(2^r)$ and
\[ (\unicode{x1D7D9}_P+i_3\eta q_4)(\tilde{\eta}_r+i_3\eta^2)=\tilde{\eta}_r+i_3\eta^2+i_3\eta^2=\tilde{\eta}_r, \]we may assume that $\epsilon _{j_1}=1$
and $\epsilon _j=0$ for $j\neq j_1$.(ii) If $w_j=1$
for some $j$, then $w_j=1$ for exactly one $j$, say $w_{j_2}=1$; in this case, $\epsilon _j=0$ for all $j$.
By (2.3) we have the equivalences for maps $S^5\to P^4(2^r)\vee C^5_s$
:
Thus we may assume that $\bar {\phi }=\tilde {\eta }_{r_{j_1}}$
if $r_{j_1}\leq r_{j_2}$
; otherwise $\bar {\phi }=i_P\tilde {\eta }_{r_{j_2}}$
, which prove the homotopy equivalences in (2).
5. Some applications
In this section we apply the homotopy decomposition of $\Sigma ^2M$
given by Theorem 1.1 to study the reduced $K$
-groups and the cohomotopy sets of $M$
.
5.1 Reduced $K$-groups
To prove Corollary 1.3 we recall that the reduced complex $K$
-group $\widetilde {K}(S^n)$
is isomorphic to ${\mathbb {Z}}$
if $n$
is even, otherwise $\widetilde {K}(S^n)=0$
; the reduced $KO$
-groups of spheres are given by
Using the reduced complex $K$
-groups and $KO$
-groups of spheres one can easily get the following lemma, where the notations $A^7(\tilde {\eta }_r)$
and $A^7(i_P\tilde {\eta }_r)$
refer to (2.4).
Lemma 5.1 Let $m,\,r$
be positive integers and let $p$
be a prime.
(1) $\widetilde {K}(P^{2m}(p^r))\cong {\mathbb {Z}/p^{r}}$
and $\widetilde {K}(P^{2m+1}(p^r))=0$.(2) $\widetilde {K}(C^{2m}_\eta )\cong {\mathbb {Z}}\oplus {\mathbb {Z}}$
and $\widetilde {K}(C^{2m+1}_\eta )=0$.(3) $\widetilde {K}(C^{6}_r)\cong \widetilde {K}(A^7(i_P\tilde {\eta }_r))\cong {\mathbb {Z}}$
, $\widetilde {K}(A^7(\tilde {\eta }_r))=0$.(4) $\widetilde {KO}^2(P^{4+i}(p^r))=\widetilde {KO}^2(C^7_\eta )=0$
for $p\geq 3$ and $i=0,\,1,\,2$.(5) $\widetilde {KO}^2(P^5(2^r))\cong \widetilde {KO}^2(A^7(\tilde {\eta }_r))\cong {\mathbb {Z}/2^{}}$
.(6) $\widetilde {KO}^2(C^6_\eta )\cong \widetilde {KO}^2(C^6_r)\cong \widetilde {KO}^2(A^7(i_P\tilde {\eta }_r))\cong {\mathbb {Z}}\oplus {\mathbb {Z}/2^{}}$
.
Proposition 5.2 Let $M$
be an orientable smooth closed five-manifold given by Theorem 1.1 or 1.2. There hold isomorphisms
Proof. We only give the proof of $\widetilde {KO}(M)$
here, because the proof of $\widetilde {K}(M)$
is similar but simpler. By Theorem 1.1 we can write
where $\Sigma ^2X\simeq (S^5\vee P^5(2^{r_{j_1}})\vee C^6_{r_{j_2}})\cup \,{\rm e}^7$
. By lemma 5.1 and the table (5.1), there is a chain of isomorphisms
where $\widetilde {KO}^2(\Sigma ^2X)\cong {\mathbb {Z}}\oplus {\mathbb {Z}/2^{}}\oplus {\mathbb {Z}/2^{}}$
in all cases of Theorem 1.1 can be easily computed by lemma 5.1.
5.2 Cohomotopy sets
Let $M$
be a closed five-manifold. It is clear that the cohomotopy Hurewicz maps
with $\iota _i\in H^i(S^i)$
a generator are isomorphisms for $i=1$
or $i\geq 5$
. For $\pi ^4(M)$
, there is a short exact sequence of abelian groups (cf. [Reference Steenrod22])
which splits if and only if there holds an equality (cf. [Reference Taylor23, Section 6.1])
The standard action of $S^3$
on $S^2=S^3/S^1$
by left translation induces a natural action of $\pi ^3(M)$
on $\pi ^2(M)$
. More concretely, the Hopf fibre sequence
induces an exact sequence of sets
where $[M,\,\mathbb {H}P^{\infty }]=\pi ^4(M)$
because $\mathbb {H}P^{\infty }$
has the $6$
-skeleton $S^4$
, $h=h^2$
is the second cohomotopy Hurewicz map. The homomorphism $\kappa _u$
in (5.2) is given by the following lemma.
Lemma 5.3 (cf. Theorem 3 of [Reference Kirby, Melvin and Teichner13])
The natural action of $\pi ^3(M)$
on $\pi ^2(M)$
is transitive on the fibres of $h$
and the stabilizer of $u\in \pi ^2(M)$
equals the image of the homomorphism
where $\Delta _M$
is the diagonal map on $M$
, $\kappa \colon S^2\times S^1\to S^3$
is the conjugation $(gS^1,\,t)\mapsto gtg^{-1}$
by setting $S^2=S^3/S^1$
.
Thus, in a certain sense we only need to determine the third cohomotopy group $\pi ^3(M)$
. Recall the EHP fibre sequence (cf. [Reference Neisendorfer20, Corollary 4.4.3])
which induces an exact sequence
where $0=[M,\,\Omega S^7]=[\Sigma M,\,S^7]$
by dimensional reason.
Lemma 5.4 Let $M$
be a $5$
-manifold given by Theorem 1.1. Then
(1) $[\Sigma ^2M,\,S^7]\cong {\mathbb {Z}}\langle q_7 \rangle$
, where $q_7$ is the canonical pinch map;(2) $[\Sigma ^2M,\,S^4]$
contains a direct summand ${\mathbb {Z}}\langle \nu _4q_7\rangle$, where $\nu _4\colon S^7\to S^4$ is the Hopf map.
Proof. By Theorem 1.1, there is a homotopy decomposition
where $U$
is a $6$
-dimensional complex and $V$
belongs to the set
Let $q_V\colon \Sigma ^2M\to V$
be the pinch map onto $V$
. Then it is clear that the pinch map $q_7$
factors as the composite $\Sigma ^2M\mathop\longrightarrow\limits^ {q_V} V\mathop\longrightarrow\limits^ {q_7 \ \text {or}\ \unicode{x1D7D9}_7} S^7$
. We immediately have the chain of isomorphisms
For the group $[\Sigma ^2M,\,S^4]$
, we show that the direct summand $[V,\,S^4]$
(through the homomorphism $q_V^{\sharp }$
) is isomorphic to ${\mathbb {Z}}\langle \nu _4q_7\rangle \oplus {\mathbb {Z}}/12$
for any $V\in \mathcal {S}$
.
If $V=S^7$
, we clearly have $[S^7,\,S^4]\cong {\mathbb {Z}}\langle \nu _4 \rangle \oplus {\mathbb {Z}}/12$
. If $V=C^7_\eta$
, then from the homotopy cofibre sequence
we have an exact sequence
Since $\eta ^\sharp$
is an isomorphism, $i_5^\sharp$
is trivial and hence $q_7^\sharp$
is an isomorphism. Thus we have
If $V=A^7(\tilde {\eta }_r)= P^5(2^{r_{j_1}})\cup _{\tilde {\eta }_{r_{j_1}}}\,{\rm e}^7$
, the homotopy cofibre sequence
implying an exact sequence
Since $[P^5(2^{r_{j_1}}),\,S^4]\cong {\mathbb {Z}/2^{}}\langle \eta q_5\rangle$
, the formula $q_5\tilde {\eta }_{r_{j_1}}=\eta$
in (2.2) then implying $\tilde {\eta }_{r_{j_1}}^\sharp$
is an isomorphism. Thus
The computations for $V=A^7(i_P\tilde {\eta }_r)$
is similar. First, it is clear that
Recall we have the composite $q_5\colon P^5(2^{r_{j_1}}) \mathop\longrightarrow\limits^ {i_P}C^6_{r_{j_1}}\mathop\longrightarrow\limits^ {q_5}S^5$
. It follows that the homomorphism $[C^6_{r_{j_1}},\,S^4]\mathop\longrightarrow\limits^ {(i_P \tilde {\eta }_{r_{j_1}})^\sharp } \pi _6(S^4)$
is an isomorphism, and thus there is an isomorphism
Lemma 5.5 Let $r\geq 1$
be an integer. There hold isomorphisms
(1) $[C^5_\eta,\,S^4]=0$
and $[C^5_r,\,S^4]\cong {\mathbb {Z}/2^{r+1}}$.(2) $[A^6(\tilde {\eta }_r),\,S^4]\cong {\mathbb {Z}/2^{r-1}}$
, where ${\mathbb {Z}}/1=0$ for $r=1$.(3) $[A^6(i_P\tilde {\eta }_r),\,S^4]\cong {\mathbb {Z}/2^{r}}$
.
Proof. (1) The groups in (1) refer to [Reference Baues2] or [Reference Li14].
(2) The homotopy cofibre sequence for $A^6(\tilde {\eta }_r)$
, as given in the proof of lemma 5.4, implying an exact sequence
Thus $(i_P)^\sharp$
is a monomorphism and $\operatorname {im} (i_P)^\sharp =\ker (\tilde {\eta }_r^\sharp )\cong {\mathbb {Z}/2^{r-1}}\langle 2q_4\rangle$
.
(3) The computation of the group $[A^6(i_P\tilde {\eta }_r),\,S^4]$
is similar, by noting the isomorphism $[C^5_r,\,S^4]\cong {\mathbb {Z}/2^{r+1}}\langle q_4\rangle$ (cf. [Reference Baues2]).
Proposition 5.6 Let $M$
be a $5$
-manifold given by Theorems 1.1 or 1.2. The homomorphism $(\Omega H)_\sharp$
in (5.3) is surjective and hence there is an isomorphism
Moreover, let $M$
be the $5$
-manifold, together with the integers $c_1,\,c_2$
and $r_{j_1}$
, given by Theorem 1.1, then we have the following concrete results:
(1) if $M$
is spin, then
\[ \pi^3(M)\cong {\mathbb{Z}}^d\oplus ({\mathbb{Z}/2^{}})^{l+1-c_1-c_2}\oplus T[c_2]\oplus \left(\bigoplus_{j=1}^{c_2}{\mathbb{Z}/2^{r_{j}+1}}\right); \]
(2) if $M$
is non-spin and the conditions in (a) hold, then
\[ \pi^3(M)\cong {\mathbb{Z}}^{d}\oplus ({\mathbb{Z}/2^{}})^{l-c_1-c_2}\oplus T[c_2]\oplus \left(\bigoplus_{j=1}^{c_2}{\mathbb{Z}/2^{r_{j}+1}}\right); \]
(3) if $M$
is non-spin and the conditions in (b) hold, then $\pi ^3(M)$ is isomorphic to one of the following groups:
\begin{align*} & (i)\quad {\mathbb{Z}}^{d}\oplus ({\mathbb{Z}/2^{}})^{l-c_1-c_2}\oplus \frac{T[c_2]}{{\mathbb{Z}/2^{r_{j_1}}}}\oplus \left(\bigoplus_{j=1}^{c_2}{\mathbb{Z}/2^{r_{j}+1}}\right)\oplus {\mathbb{Z}/2^{r_{j_1}-1}},\\ & (ii)\quad{\mathbb{Z}}^{d}\oplus ({\mathbb{Z}/2^{}})^{l-c_1-c_2}\oplus T[c_2]\oplus \left(\bigoplus_{j_1\neq j=1}^{c_2}{\mathbb{Z}/2^{r_{j}+1}}\right)\oplus {\mathbb{Z}/2^{r_{j_1}}}. \end{align*}
Proof. We first apply the exact sequence (5.3) to show that the suspension $\pi ^3(M)\mathop\longrightarrow\limits^ {\Sigma }\pi ^4(\Sigma M)$
is an isomorphism. By duality, it suffices to show the second James–Hopf invariant $H$
induces a surjection $H_\sharp \colon [\Sigma ^2M,\,S^4]\to [\Sigma ^2M,\,S^7].$
By lemma 5.4, there hold isomorphisms
for some abelian group $G$
. Then the surjectivity of $H_\sharp$
follows by the homotopy equalities
Note the first statement only depends the homotopy type of the double suspension $\Sigma ^2M$
, so we can also assume that $M$
is the five-manifold satisfying conditions in Theorem 1.1.
The computations of the group $[\Sigma M,\,S^4]$
follows by Theorem 1.1, lemma 5.5:
(1) If $M$
is spin, then
\begin{align*} [\Sigma M,S^4]& \cong \left(\bigoplus_{i=1}^d[S^4,S^4]\right)\oplus \left(\bigoplus_{i=1}^{l-c_1-c_2}[S^5,S^4]\right)\oplus [P^4(T[c_2]),S^4]\\ & \oplus \left(\bigoplus_{j=1}^{c_2}[C^5_{r_{j}},S^4]\right)\oplus [S^6,S^4]. \end{align*}
(2) If $M$
is non-spin and $\Sigma M$ is given by (a), then
\begin{align*} [\Sigma M,S^4]& \cong \left(\bigoplus_{i=2}^d[S^4,S^4]\right)\oplus \left(\bigoplus_{i=1}^{l-c_1-c_2}[S^5,S^4]\right)\oplus [P^4(T[c_2]),S^4]\\ & \oplus \left(\bigoplus_{j=1}^{c_2}[C^5_{r_{j}},S^4]\right)\oplus [C^6_\eta,S^4]. \end{align*}
(3) If $M$
is non-spin and $\Sigma M$ is given by (b), then
\begin{align*} [\Sigma M,S^4]& \cong \left(\bigoplus_{i=1}^d[S^4,S^4]\right)\oplus \left(\bigoplus_{i=1}^{l-c_1-c_2}[S^5,S^4]\right)\oplus [P^4\left(\frac{T[c_2]}{{\mathbb{Z}/2^{r_{j_1}}}}\right),S^4]\\ & \oplus \left(\bigoplus_{j=1}^{c_2}[C^5_{r_{j}},S^4]\right)\oplus [A^6(\tilde{\eta}_{r_{j_1}}),S^4], \end{align*}or
\begin{align*} [\Sigma M,S^4]& \cong \left(\bigoplus_{i=1}^d[S^4,S^4]\right)\oplus \left(\bigoplus_{i=1}^{l-c_1-c_2}[S^5,S^4]\right)\oplus [P^4(T[c_2]),S^4]\\ & \oplus \left(\bigoplus_{j_1\neq j=1}^{c_2}[C^5_{r_{j}},S^4]\right)\oplus [A^6(i_P\tilde{\eta}_{r_{j_1}}),S^4].\end{align*}
Acknowledgements
The authors would like to thank the reviewer(s) for the new and faster proof of lemma 2.3 (2). Pengcheng Li and Zhongjian Zhu were supported by National Natural Science Foundation of China under Grant 1210 1290 and 11701430, respectively.
