Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T11:44:27.520Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent wake behind side-by-side flat plates: computational study of interference effects

Published online by Cambridge University Press:  24 September 2018

Fatemeh H. Dadmarzi Open the ORCID record for Fatemeh H. Dadmarzi [Opens in a new window] ,
Vagesh D. Narasimhamurthy Open the ORCID record for Vagesh D. Narasimhamurthy [Opens in a new window] ,
Helge I. Andersson  and
Bjørnar Pettersen
Fatemeh H. Dadmarzi*
Affiliation:
Department of Marine Technology, Norwegian University of Science and Technology, NO-7491, Trondheim, Norway
Vagesh D. Narasimhamurthy
Affiliation:
Department of Applied Mechanics, Indian Institute of Technology Madras, Chennai 600036, India
Helge I. Andersson
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, NO-7491, Trondheim, Norway
Bjørnar Pettersen
Affiliation:
Department of Marine Technology, Norwegian University of Science and Technology, NO-7491, Trondheim, Norway
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The complex wake behind two side-by-side flat plates placed normal to the inflow direction has been explored in a direct numerical simulation study. Two gaps, 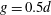$g=0.5d$ and 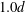$1.0d$, were considered, both at a Reynolds number of 1000 based on the plate width 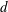$d$ and the inflow velocity. For gap ratio 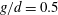$g/d=0.5$, the biased gap flow resulted in an asymmetric flow configuration consisting of a narrow wake with strong vortex shedding and a wide wake with no periodic near-wake shedding. Shear-layer transition vortices were observed in the wide wake, with characteristic frequency 0.6. For 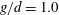$g/d=1.0$, two simulations were performed, started from a symmetric and an asymmetric initial flow field. A symmetric configuration of Kármán vortices resulted from the first simulation. Surprisingly, however, two different three-dimensional instability features were observed simultaneously along the span of the upper and lower plates. The spanwise wavelengths of these secondary streamwise vortices, formed in the braid regions of the primary Kármán vortices, were approximately 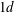$1d$ and 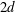$2d$, respectively. The wake bursts into turbulence some 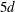$5d$–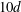$10d$ downstream. The second simulation resulted in an asymmetric wake configuration similar to the asymmetric wake found for the narrow gap 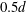$0.5d$, with the appearance of shear-layer instabilities in the wide wake. The analogy between a plane mixing layer and the separated shear layer in the wide wake was examined. The shear-layer frequencies obtained were in close agreement with the frequency of the most amplified wave based on linear stability analysis of a plane mixing layer.

JFM classification

Vortex Flows: Vortex dynamics Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 1040 - 1073
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akinaga, T. & Mizushima, J. 2005 Linear stability of flow past two circular cylinders in a side-by-side arrangement. J. Phys. Soc. Japan 74, 1366–1369.Google Scholar
Alam, M. M. & Zhou, Y. 2013 Intrinsic features of flow around two side-by-side square cylinders. Phys. Fluids 25, 085106.Google Scholar
Alam, M. M., Zhou, Y. & Wang, X. W. 2011 The wake of two side-by-side square cylinders. J. Fluid Mech. 669, 432–471.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Bearman, P. W. & Wadcock, A. J. 1973 The interaction between a pair of circular cylinders normal to a stream. J. Fluid Mech. 61, 499–511.Google Scholar
Bernal, L. P. & Roshko, A. 1986 Streamwise vortex structure in plane mixing layers. J. Fluid Mech. 170, 499–525.Google Scholar
Bloor, M. S. 1964 The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 19, 290–304.Google Scholar
Brun, C., Tenchine, D. & Hopfinger, E. J. 2004 Role of the shear layer instability in the near wake behavior of two side-by-side circular cylinders. Exp. Fluids 36, 334–343.Google Scholar
Carmo, B. S., Meneghini, J. R. & Sherwin, S. J. 2010a Secondary instabilities in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.Google Scholar
Carmo, B. S., Meneghini, J. R. & Sherwin, S. J. 2010b Possible states in the flow around two circular cylinders in tandem with separations in the vicinity of the drag inversion spacing. Phys. Fluids 22, 054101.Google Scholar
Carmo, B. S., Sherwin, S. J., Bearman, P. W. & Willden, R. H. J. 2008 Wake transition in the flow around two circular cylinders in staggered arrangements. J. Fluid Mech. 597, 1–29.Google Scholar
Castro, I. 1971 Wake characteristics of two-dimensional perforated plate normal to an air-stream. J. Fluid Mech. 46, 599–609.Google Scholar
Choi, C.-B., Jang, Y.-J. & Yang, K.-S. 2012 Secondary instability in the near-wake past two tandem square cylinders. Phys. Fluids 24, 024102.Google Scholar
Choi, C.-B. & Yang, K.-S. 2013 Three-dimensional instability in the flow past two side-by-side square cylinders. Phys. Fluids 25, 074107.Google Scholar
Cimbala, J. M., Nagib, H. M. & Roshko, A. 1988 Large structure in the far wakes of two-dimensional bluff bodies. J. Fluid Mech. 190, 265–298.Google Scholar
Dadmarzi, F. H., Narasimhamurthy, V. D., Andersson, H. I. & Pettersen, B. 2011 The turbulent wake behind side-by-side plates. J. Phys. Conf. Ser. 318, 062010.Google Scholar
Gerrard, J. H. 1966 The mechanics of the formation region of vortices behind bluff bodies. J. Fluid Mech. 25, 401–413.Google Scholar
Hayashi, M., Sakurai, A. & Ohya, Y. 1986 Wake interference of a row of normal flat plates arranged side by side in a uniform flow. J. Fluid Mech. 164, 1–25.Google Scholar
Hemmati, A., Wood, D. H. & Martinuzzi, R. J. 2016 Characteristics of distinct flow regimes in the wake of an infinite span normal thin flat plate. Intl J. Heat Fluid Flow 62 (Part B), 423–436.Google Scholar
Higuchi, H., Lewalle, J. & Crane, P. 1994 On the structure of a two-dimensional wake behind a pair of flat plates. Phys. Fluids 6, 297–305.Google Scholar
Ho, C.-M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16, 365–422.Google Scholar
Huang, Z., Ferré, J. A., Kawall, J. G. & Keffer, J. F. 1995 The connection between near and far regions of the turbulent porous body wake. Exp. Therm Fluid Sci. 11 (2), 143–154.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
Inoue, O. 1985 A new approach to flow problems past a porous plate. AIAA J. 23, 1916–1921.Google Scholar
Kim, H. J. & Durbin, P. A. 1988 Investigation of the flow between a pair of circular cylinders in the flopping regime. J. Fluid Mech. 196, 431–448.Google Scholar
Koch, W. 1985 Local instability characteristics and frequency determination of self-excited wake flows. J. Sound Vib. 99, 53–83.Google Scholar
Kochin, N. E., Kibel, I. A. & Roze, N. V. 1964 Theoretical Hydrodynamics. Wiley Interscience (translated from the fifth Russian edition).Google Scholar
Kolar, V., Lyn, D. A. & Rodi, W. 1997 Ensemble-averaged measurements in the turbulent near wake of two side-by-side square cylinders. J. Fluid Mech. 346, 201–237.Google Scholar
Landweber, L.1942 Flow about a pair of adjacent, parallel cylinders normal to a stream. Tech. Rep. 485. Navy Department, David W. Taylor Model Basin.Google Scholar
Manhart, M. 2004 A zonal grid algorithm for DNS of turbulent boundary layers. Comput. Fluids 33, 435–461.Google Scholar
Mathis, M., Provansal, M. & Boyer, L. 1984 Bénard–von Kármán instability: an experimental study near the threshold. J. Phys. Lett. Paris 45, 483–491.Google Scholar
Meiburg, E. & Lasheras, J. C. 1988 Experimental and numerical investigation of the three-dimensional transition in plane wakes. J. Fluid Mech. 190, 1–37.Google Scholar
Miau, J. J., Wang, G. Y. & Chou, J. H. 1992 Intermittent switching of gap flow downstream of two flat plates arranged side by side. J. Fluids Struct. 6, 563–582.Google Scholar
Miau, J. J., Wang, H. B. & Chou, J. H. 1996 Flopping phenomenon of flow behind two plates placed side-by-side normal to the flow direction. Fluid Dyn. Res. 17, 311–328.Google Scholar
Mizushima, J. & Hatsuda, G. 2014 Nonlinear interactions between the two wakes behind a pair of square cylinders. J. Fluid Mech. 750, 295–320.Google Scholar
Najjar, F. M. & Balachandar, S. 1998 Low-frequency unsteadiness in the wake of a normal flat plate. J. Fluid Mech. 370, 101–147.Google Scholar
Najjar, F. M. & Vanka, S. P. 1995 Effects of intrinsic three-dimensionality on the drag characteristics of a normal flat plate. Phys. Fluids 7, 2516–2518.Google Scholar
Narasimhamurthy, V. D. & Andersson, H. I. 2009 Numerical simulation of the turbulent wake behind a normal flat plate. Intl J. Heat Fluid Flow 30, 1037–1043.Google Scholar
Peller, N., Duc, A. L., Tremblay, F. & Manhart, M. 2006 High-order stable interpolations for immersed boundary methods. Intl J. Numer. Meth. Fluids 52, 1175–1193.Google Scholar
Prasad, A. & Williamson, C. H. 1997 The instability of the shear layer separating from a bluff body. J. Fluid Mech. 333, 375–402.Google Scholar
Radi, A., Thompson, M. C., Rao, A., Hourigan, K. & Sheridan, J. 2013 Experimental evidence of new three-dimensional modes in the wake of a rotating cylinder. J. Fluid Mech. 734, 567–594.Google Scholar
Robichaux, J., Balachandar, S. & Vanka, S. P. 1999 Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 11, 560–578.Google Scholar
Strykowski, P. J.1986 The control of absolutely and convectively unstable shear flows. PhD thesis, Yale University, New Haven.Google Scholar
Sumner, D. 2010 Two circular cylinders in cross-flow: a review. J. Fluids Struct. 26, 849–899.Google Scholar
Sumner, D., Wong, S. S. T., Price, S. J. & Paidoussis, M. P. 1999 Fluid behaviour of side-by-side circular cylinders in steady cross-flow. J. Fluids Struct. 13, 309–338.Google Scholar
Thompson, M. C., Hourigan, K., Ryan, K. & Sheard, G. J. 2006 Wake transition of two-dimensional cylinders and axisymmetric bluff bodies. J. Fluids Struct. 22, 793–806.Google Scholar
Unal, M. F. & Rockwell, D. 1988a On vortex formation from a cylinder. Part 1. The initial instability. J. Fluid Mech. 190, 491–512.Google Scholar
Wei, T. & Smith, C. R. 1986 Secondary vortices in the wake of circular cylinders. J. Fluid Mech. 169, 513–533.Google Scholar
Williamson, C. H. K. 1985 Evolution of a single wake behind a pair of bluff bodies. J. Fluid Mech. 159, 1–18.Google Scholar
Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Winant, C. D. & Browand, F. K. 1974 Vortex pairing: the mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 63, 237–255.Google Scholar
Wood, C. J. 1964 The effect of base bleed on a periodic wake. J. R. Aero. Soc. 68, 477–482.Google Scholar
Xu, S. J., Zhou, Y. & So, R. M. C. 2003 Reynolds number effects on the flow structure behind two side-by-side cylinders. Phys. Fluids 15, 1214–1219.Google Scholar
Yen, S. C. & Liu, J. H. 2011 Wake flow behind two side-by-side square cylinders. Intl J. Heat Fluid Flow 32, 41–51.Google Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013 Mode C flow transition behind a circular cylinder with a near-wake wire disturbance. J. Fluid Mech. 727, 30–55.Google Scholar
Zdravkovich, M. M. 1977 REVIEW: review of flow interference between two circular cylinders in various arrangements. Trans. ASME J. Fluids Engng 99, 618–633.Google Scholar
Zhang, H.-Q., Fey, U., Noack, B. R., König, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7, 779–794.Google Scholar
Zhou, Y. 2003 Vortical structures behind three side-by-side cylinders. Exp. Fluids 34, 68–76.Google Scholar
Zhou, Y. & Alam, M. M. 2016 Wake of two interacting circular cylinders: a review. Intl J. Heat Fluid Flow 62, 510–537.Google Scholar