Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T12:07:32.273Z Has data issue: false hasContentIssue false
  • English
  • Français

Global linear stability analysis of jets in cross-flow

Published online by Cambridge University Press:  12 September 2017

Marc A. Regan  and
Krishnan Mahesh Open the ORCID record for Krishnan Mahesh [Opens in a new window]
Marc A. Regan
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Krishnan Mahesh
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability of low-speed jets in cross-flow (JICF) is studied using tri-global linear stability analysis (GLSA). Simulations are performed at a Reynolds number of 2000, based on the jet exit diameter and the average velocity. A time stepper method is used in conjunction with the implicitly restarted Arnoldi iteration method. GLSA results are shown to capture the complex upstream shear-layer instabilities. The Strouhal numbers from GLSA match upstream shear-layer vertical velocity spectra and dynamic mode decomposition from simulation (Iyer & Mahesh, J. Fluid Mech., vol. 790, 2016, pp. 275–307) and experiment (Megerian et al., J. Fluid Mech., vol. 593, 2007, pp. 93–129). 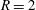Additionally, the GLSA results are shown to be consistent with the transition from absolute to convective instability that the upstream shear layer of JICFs undergoes between $R=2$ to 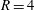$R=4$ observed by Megerian et al. (J. Fluid Mech., vol. 593, 2007, pp. 93–129), where 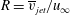$R=\overline{v}_{jet}/u_{\infty }$ is the jet to cross-flow velocity ratio. The upstream shear-layer instability is shown to dominate when 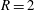$R=2$, whereas downstream shear-layer instabilities are shown to dominate when 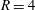$R=4$.

JFM classification

Instability: Absolute/convective instability Wakes/Jets: Jets Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 812 - 836
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18 (6), 068102.CrossRefGoogle Scholar
Alves, L. S. De B., Kelly, R. E. & Karagozian, A. R. 2008 Transverse-jet shear-layer instabilities. Part 2. Linear analysis for large jet-to-cross-flow velocity ratio. J. Fluid Mech. 602 (2008), 383–401.CrossRefGoogle Scholar
Arnoldi, W. E. 1951 The principle of minimized iteration in the solution of the matrix eigenproblem. Q. Appl. Maths 9, 17–29.CrossRefGoogle Scholar
Babu, P. C. & Mahesh, K. 2004 Upstream entrainment in numerical simulations of spatially evolving round jets. Phys. Fluids 16 (10), 3699–3705.CrossRefGoogle Scholar
Bagheri, S., Schlatter, P., Schmid, P. J. & Henningson, D. S. 2009 Global stability of a jet in cross-flow. J. Fluid Mech. 624, 33–44.CrossRefGoogle Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.CrossRefGoogle Scholar
Coelho, S. L. V. & Hunt, J. C. R. 1989 The dynamics of the near field of strong jets in cross-flows. J. Fluid Mech. 200, 95–120.CrossRefGoogle Scholar
Crighton, D. G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 77, 397–413.CrossRefGoogle Scholar
Criminale, W. O., Jackson, T. L. & Joslin, R. D. 2003 Theory and Computation of Hydrodynamic Stability. Cambridge Univesity Press.CrossRefGoogle Scholar
Ding, Y. & Kawahara, M. 1998 Linear stability of incompressible flow using a mixed finite element method. J. Comput. Phys. 273, 243–273.CrossRefGoogle Scholar
Eiff, O. S., Kawall, J. G. & Keffer, J. F. 1995 Lock-in of vortices in the wake of an elevated round turbulent jet in a cross-flow. Exp. Fluids 19 (3), 203–213.CrossRefGoogle Scholar
Fric, T. F. & Roshko, A. 1994 Vortical structure in the wake of a transverse jet. J. Fluid Mech. 279, 1–47.CrossRefGoogle Scholar
Giannetti, F., Luchini, L. & Marino, L. 2009 Linear stability analysis of three-dimensional lid-driven cavity flow. In Proceedings of the 19th Congress of the Italian Association of Theoretical and Applied Mechanics, 14–17 September, 2009, Aras Edizioni, Ancona, Italy, pp. 738.1–738.10.Google Scholar
Gómez, F., Gómez, R. & Theofilis, V. 2014 On three-dimensional global linear instability analysis of flows with standard aerodynamics codes. Aerosp. Sci. Technol. 32 (1), 223–234.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in open shear layers. J. Fluid Mech. 159, 151–168.CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. Center for Turbulence Research, Proc. Summer Program (1970), pp. 193–208.Google Scholar
Iyer, P. S. & Mahesh, K. 2016 A numerical study of shear layer characteristics of low-speed transverse jets. J. Fluid Mech. 790 (2016), 275–307.CrossRefGoogle Scholar
Jordan, P. & Colonius, T. 2013 Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 45 (1), 173–195.CrossRefGoogle Scholar
Juniper, M. P., Hanifi, A. & Theofilis, V. 2014 Modal stability theory lecture notes from the flow-nordita summer school on advanced instability methods for complex flows, Stockholm, Sweden. Appl. Mech. Rev. 66 (2).Google Scholar
Kamotani, Y. & Greber, I. 1972 Experiments on a turbulent jet in a cross flow. AIAA J. 10 (11), 1425–1429.CrossRefGoogle Scholar
Karagozian, A. R. 2010 Transverse jets and their control. Prog. Energy Combust. Sci. 36 (5), 531–553.CrossRefGoogle Scholar
Kelso, R. M., Lim, T. T. & Perry, A. E. 1996 An experimental study of round jets in cross-flow. J. Fluid Mech. 306, 111–144.CrossRefGoogle Scholar
Kelso, R. M. & Smits, A. J. 1995 Horseshoe vortex systems resulting from the interaction between a laminar boundary layer and a transverse jet. Phys. Fluids 7 (1), 153–158.CrossRefGoogle Scholar
Krothapalli, A., Lourenco, L. & Buchlin, J. M 1990 Separated flow upstream of a jet in a cross-flow. AIAA J. 28 (3), 414–420.Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C.1997 ARPACK Users’ Guide: Solution of Large Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods.CrossRefGoogle Scholar
Mahesh, K. 2013 The interaction of jets with cross-flow. Annu. Rev. Fluid Mech. 45 (1), 379–407.CrossRefGoogle Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197 (1), 215–240.CrossRefGoogle Scholar
Margason, R. J. 1993 Fifty years of jet in cross flow research. Advisory Group for Aerospace Research & Development Conference, vol. 534, pp. 1–41.Google Scholar
M’Closkey, R. T., King, J. M., Cortelezzi, L. & Karagozian, A. R. 2002 The actively controlled jet in cross-flow. J. Fluid Mech. 452, 325–335.CrossRefGoogle Scholar
McMahon, H. M., Hester, D. D. & Palfery, J. G. 1971 Vortex shedding from a turbulent jet in a cross-wind. J. Fluid Mech. 48 (1), 73–80.CrossRefGoogle Scholar
Megerian, S., Davitian, J., Alves, L. S. De B. & Karagozian, A. R. 2007 Transverse-jet shear-layer instabilities. Part 1. Experimental studies. J. Fluid Mech. 593, 93–129.CrossRefGoogle Scholar
Moussa, Z. M., Trischka, J. W. & Eskinazi, D. S. 1977 The near field in the mixing of a round jet with a cross-stream. J. Fluid Mech. 80 (1), 49–80.CrossRefGoogle Scholar
Muppidi, S. & Mahesh, K. 2005 Study of trajectories of jets in cross-flow using direct numerical simulations. J. Fluid Mech. 530, 81–100.CrossRefGoogle Scholar
Muppidi, S. & Mahesh, K. 2007 Direct numerical simulation of round turbulent jets in cross-flow. J. Fluid Mech. 574, 59–84.CrossRefGoogle Scholar
Muppidi, S. & Mahesh, K. 2008 Direct numerical simulation of passive scalar transport in transverse jets. J. Fluid Mech. 598, 335–360.CrossRefGoogle Scholar
Narayanan, S., Barooah, P. & Cohen, J. M. 2003 Dynamics and control of an isolated jet in cross-flow. AIAA J. 41 (12), 2316–2330.CrossRefGoogle Scholar
Peplinski, A., Schlatter, P. & Henningson, D. S. 2015 Global stability and optimal perturbation for a jet in cross-flow. Eur. J. Mech. (B/Fluids) 49, 438–447.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows, 1st edn. Cambridge University Press.CrossRefGoogle Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.CrossRefGoogle Scholar
Sau, R. & Mahesh, K. 2007 Passive scalar mixing in vortex rings. J. Fluid Mech. 582, 449.Google Scholar
Sau, R. & Mahesh, K. 2008 Dynamics and mixing of vortex rings in cross-flow. J. Fluid Mech. 604, 389–409.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 1979 Boundary-layer Theory, 7th edn. McGraw Hill.Google Scholar
Shapiro, S. R., King, J., M’Closkey, R. T. & Karagozian, A. R. 2006 Optimization of controlled jets in cross-flow. AIAA J. 44 (6), 1292–1298.Google Scholar
Smith, S. H. & Mungal, M. G. 1998 Mixing, structure and scaling of the jet in cross-flow. J. Fluid Mech. 357 (1998), 83–122.CrossRefGoogle Scholar
Tammisola, O. & Juniper, M. P. 2016 Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43 (1), 319–352.CrossRefGoogle Scholar
Turton, S. E., Tuckerman, L. S. & Barkley, Dwight 2015 Prediction of frequencies in thermosolutal convection from mean flows. Phys. Rev. E 91 (4), 1–10.CrossRefGoogle ScholarPubMed
Vyazmina, E.2010 Bifurcations in a swirling flow. PhD thesis, École Polytechnique.Google Scholar