Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T11:37:43.904Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal perturbation for two-dimensional vortex systems: route to non-axisymmetric state

Published online by Cambridge University Press:  21 September 2018

Navrose Open the ORCID record for Navrose [Opens in a new window] ,
H. G. Johnson ,
V. Brion ,
L. Jacquin  and
J. C. Robinet
Navrose*
Affiliation:
Département Aérodynamique Aéroélasticité Aéroacoustique, ONERA, 92190 Meudon, France Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur 208 016, UP, India
H. G. Johnson
Affiliation:
Département Aérodynamique Aéroélasticité Aéroacoustique, ONERA, 92190 Meudon, France
V. Brion
Affiliation:
Département Aérodynamique Aéroélasticité Aéroacoustique, ONERA, 92190 Meudon, France
L. Jacquin
Affiliation:
Département Aérodynamique Aéroélasticité Aéroacoustique, ONERA, 92190 Meudon, France
J. C. Robinet
Affiliation:
DynFluid Laboratory, Arts et Métiers ParisTech, 75013 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate perturbations that maximize the gain of disturbance energy in a two-dimensional isolated vortex and a counter-rotating vortex pair. The optimization is carried out using the method of Lagrange multipliers. For low initial energy of the perturbation (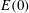$E(0)$), the nonlinear optimal perturbation/gain is found to be the same as the linear optimal perturbation/gain. Beyond a certain threshold 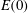$E(0)$, the optimal perturbation/gain obtained from linear and nonlinear computations are different. There exists a range of 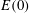$E(0)$ for which the nonlinear optimal gain is higher than the linear optimal gain. For an isolated vortex, the higher value of nonlinear optimal gain is attributed to interaction among different azimuthal components, which is otherwise absent in a linearized system. Spiral dislocations are found in the nonlinear optimal perturbation at the radial location where the most dominant wavenumber changes. Long-time nonlinear evolution of linear and nonlinear optimal perturbations is studied. The evolution shows that, after the initial increment of perturbation energy, the vortex attains a quasi-steady state where the mean perturbation energy decreases on a slow time scale. The quasi-steady vortex state is non-axisymmetric and its shape depends on the initial perturbation. It is observed that the lifetime of a quasi-steady vortex state obtained using the nonlinear optimal perturbation is longer than that obtained using the linear optimal perturbation. For a counter-rotating vortex pair, the mechanism that maximizes the energy gain is found to be similar to that of the isolated vortex. Within the linear framework, the optimal perturbation for a vortex pair can be either symmetric or antisymmetric, whereas the structure of the nonlinear optimal perturbation, beyond the threshold 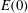$E(0)$, is always asymmetric. No quasi-steady state for a counter-rotating vortex pair is observed.

JFM classification

Instability: Nonlinear instability Vortex Flows: Vortex dynamics Vortex Flows: Vortex instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 922 - 952
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antkowiak, A. & Brancher, P. 2004 Transient energy growth for the Lamb–Oseen vortex. Phys. Fluids 16 (1), L1–L4.Google Scholar
Antkowiak, A. & Brancher, P. 2007 On vortex rings around vortices: an optimal mechanism. J. Fluid Mech. 578, 295–304.Google Scholar
Barkley, D. 2016 Theoretical perspective on the route to turbulence in a pipe. J. Fluid Mech. 803, P1.Google Scholar
Bernoff, A. J. & Lingevitch, J. F. 1994 Rapid relaxation of an axisymmteric vortex. Phys. Fluids 6 (11), 3717–3723.Google Scholar
Bisanti, L.2013 Linear and nonlinear optimal perturbation analysis of vortices in incompressible flows. PhD Thesis, Institute National Polytechnique de Toulouse, Université de Toulouse.Google Scholar
Brion, V.2009 Stabilité de paires de tourbillons contra-rotatifs: application au tourbillon de jeu dans les turbomachines. PhD Thesis, École Poytechnique, Palaiseau.Google Scholar
Brion, V., Sipp, D. & Jacquin, L. 2014 Linear dynamics of the Lamb–Chaplygin dipole in the two-dimensional limit. Phys. Fluids 26 (6), 064103.Google Scholar
Cherubini, S., De Palma, P., Robinet, J.-C. & Bottaro, A. 2011 The minimal seed of turbulent transition in the boundary layer. J. Fluid Mech. 689, 221–253.Google Scholar
Cherubini, S. & De Palma, P. 2013 Nonlinear optimal perturbations in a Couette flow: bursting and transition. J. Fluid Mech. 716, 251–279.Google Scholar
Corbett, P. & Bottaro, A. 2000 Optimal perturbations for bondary layers subject to streamwise pressure gradient. Phys. Fluids 12, 120–130.Google Scholar
Crow, S. C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8 (12), 2172–2179.Google Scholar
Douglas, S. C., Amari, S.-I. & Kung, S.-Y. 2000 On gradient adaptation with unit-norm constraints. IEEE Trans. Signal Process. 48 (6), 1843–1847.Google Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.Google Scholar
Farrell, B. F. 1988 Optimal excitation of perturbations in viscous shear flow. Phys. Fluids 31 (8), 2093–2102.Google Scholar
Fischer, P., Lottes, J. & Kerkemeier, S.2008 Nek5000 webpage. http://nek5000.mcs.anl.gov.Google Scholar
Green, S. I. 1995 Fluid Vortices. Kluwer Academic.Google Scholar
Habermann, R. 1972 Critical layers in parallel flows. Stud. Appl. Maths 51 (2), 139–161.Google Scholar
Jugier, R.2016 Stabilité bidimensionnelle de modeles de sillage d’aéronefs. PhD Thesis, Institut Supérieur de l’Aéronautique et de l’Espace, Université de Toulouse.Google Scholar
Kelvin, Lord 1880 Vibrations of a columnar vortex. Phil. Mag. 10 (61), 155–168.Google Scholar
Kerswell, R. R. 2018 Nonlinear nonmodal stability theory. Annu. Rev. Fluid Mech. 50 (1), 319–345.Google Scholar
Küchemann, D. 1965 Report on the IUTAM symposium on concentrated vortex motions in fluids. J. Fluid Mech. 21 (1), 1–20.Google Scholar
Le Dizes, S. 2000 Non-axisymmetric vortices in two-dimensional flows. J. Fluid Mech. 406, 175–198.Google Scholar
Lugt, H. J. 1983 Vortex Flow in Nature and Technology. Wiley.Google Scholar
Mao, X. & Sherwin, S. 2011 Continuous spectra of the Batchelor vortex. J. Fluid Mech. 681, 1–23.Google Scholar
Mao, X. & Sherwin, S. 2012 Transient growth associated with continuous spectra of the Batchelor vortex. J. Fluid Mech. 697, 35–59.Google Scholar
Orr, W. McF. 1907 Stability or instability of the steady motions of a perfect liquid. Proc. Ir. Acad. Sect. A 27, 9–69.Google Scholar
Pierrehumbert, R. 1980 A family of steady, translating vortex pairs with distributed vorticity. J. Fluid Mech. 99 (1), 129–144.Google Scholar
Pradeep, D. S. & Hussain, F. 2006 Transient growth of perturbations in a vortex column. J. Fluid Mech. 550, 251–288.Google Scholar
Rossi, L. F., Lingevitch, J. F. & Bernoff, A. J. 1997 Quasi-steady monopole and tripole attractors for relaxing vortices. Phys. Fluids 9 (8), 2329–2338.Google Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Schmid, P. J. & Brandt, L. 2014 Analysis of fluid systems: stability, receptivity, sensitivity. Lecture Notes from the FLOW-NORDITA Summer School on Advanced Instability Methods for Complex Flows, Stockholm, Sweden, 2013. Appl. Mech. Rev. 66 (2), 024803.Google Scholar
Sipp, D., Jacquin, L. & Cossu, C. 2000 Self-adaptation and viscous selection in concentrated two-dimensional vortex dipoles. Phys. Fluids 12 (2), 245–248.Google Scholar
Trefethen, L., Trefethen, A., Reddy, S. & Driscoll, T. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.Google Scholar
Tsai, C.-Y. & Widnall, S. E. 1976 The stability of short waves on a straight vortex filament in a weak externally imposed strain field. J. Fluid Mech. 73 (04), 721–733.Google Scholar
Zuccher, S., Bottaro, A. & Luchini, P. 2006 Algebraic growth in a Blasius boundary layer: nonlinear optimal disturbances. Eur. J. Mech. (B/Fluids) 25, 1–17.Google Scholar